Was sind Exponentialfunktionen? - Erklärung und Aufgaben
Exponentialfunktion - Definition
Die Exponentialfunktionen sind, wie der Name schon vermuten lässt, Funktionen, bei denen es insbesondere um den Exponenten geht. Dieser hat nämlich die Eigenschaft, dass er nicht eine Zahl, sondern das $x$ beinhaltet und eine Zahl die sogenannte Basis bildet. Beispiele bzw. verschiedene Schreibweisen haben wir dir im Folgenden aufgelistet:
Exponentialfunktionen - Verschiedene Schreibweisen
Beispiel
- $f(x) = 2^x$,
- $f(x) = 77^{4x}$,
- $f(x) = -5^{-x}$.
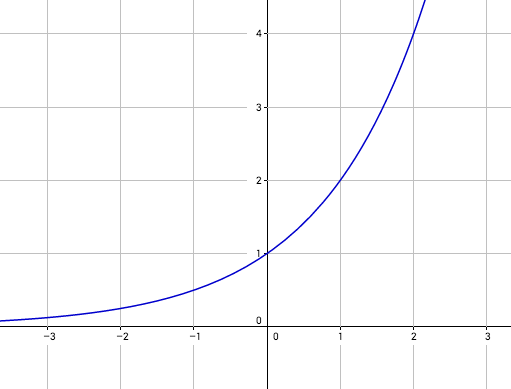
Bei dem ersten Beispiel ist die Zahl 2 die Basis und x der Exponent. Wenn wir diese Funktion einmal einzeichnen bekommen wir folgenden Funktionsgraphen:
Wir erkennen, dass die Funktion doch große Unterschiede zur quadratischen bzw. den anderen Potenzfunktionen aufweißt. Aus dem Bild können wir ablesen, dass die Funktion die x-Achse nicht trifft, sich ihr aber bei negativen x-Werten immer weiter nähert. Zudem geht die Funktion nicht durch den Ursprung, sondern durch den Punkt P(0|1).
Zusammenfassend können wir sagen:
Eigenschaften von Exponentialfunktionen
Nachfolgend zeigen wir dir die typischen Eigenschaften von Exponentialfunkionen. Dabei unterscheiden wir in Exponentialfunktionen mit einer negativen Basis und einer positiven Basis.
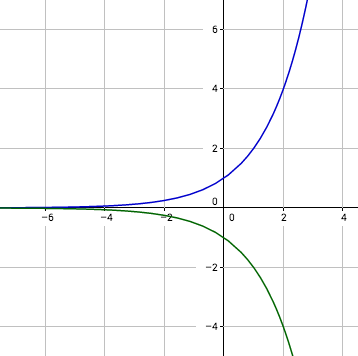
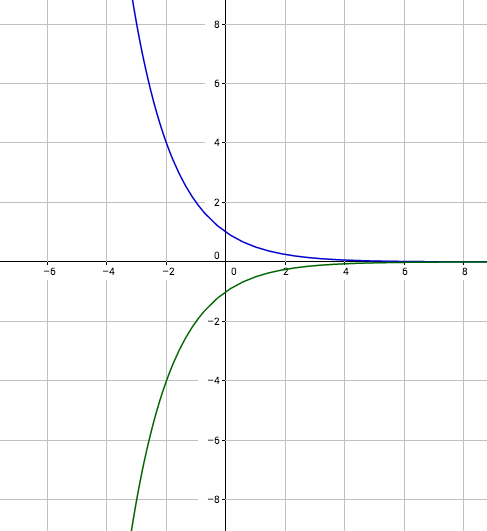
Positive Basis
Merke
Für Exponentialfunktionen bildet die x-Achse eine Asymptote.
Die Funktion zeigt kein Symmetrieverhalten.
Die Funktion hat keine Nullstellen.
Die Funktionen treffen sich alle in dem Punkt P(0|1).
Die Funktion ist bei positivem Vorzeichen von x steigend, bei negativem fallend, jedoch immer in den ersten beiden Sektoren.
Negative Basis
Bei einem negativem Vorzeichen vor der Basis sieht die Funktion schon wieder etwas anders aus. Diese sieht der Funktion mit der positiven Basis sehr ähnlich, sie ist an der y-Achse einfach gespiegelt worden und verläuft jetzt nicht auf- sondern abwärts. Die Eigenschaften sind jedoch fast alle gleich und wie folgt:
Merke
Für Exponentialfunktionen bildet die x-Achse eine Asymptote.
Die Funktion zeigt kein Symmetrieverhalten.
Die Funktion hat keine Nullstellen.
Die Funktionen treffen sich alle in dem Punkt P(0|-1).
Die Funktion ist bei positivem Vorzeichen steigend, bei negativem fallend.
Verschiebungen von Exponentialfunktionen
Eine weitere wichtige Eigenschaft kann der Streckungsfaktor sein. Dieser wird durch einen Wert vor der Basis, welcher mit dieser multipliziert wird, geschrieben. Das sähe dann so aus:
Beispiel
$f(x)= 5 \cdot 2^x$
Hierbei wird der Graph um den Faktor 5 gestreckt, und es entsteht somit eine Funktion, die nicht nur fünfmal steiler verläuft, sondern auch die y-Achse nicht bei Punkt P(1|0), sondern bei P(5|0) schneidet. Der Streckungsfaktor ändert also auch den Schnittpunkt mit der y-Achse.
Was ist jedoch mit Funktionen, die so aussehen:
$f(x)= 2^x - 7$
Diese Funktionen können auch auftreten und eine Verschiebung tritt auch hier auf. Diese Verschiebung ist je nach Vorzeichen vor der Zahl eine Verschiebung nach "oben" oder nach "unten". Es kann also vorkommen, dass ein Graph mit solch einer Schreibweise eine Nullstelle hat, weil er auf der y-Achse in negative Richtung verschoben wurde.
Zuletzt kann natürlich auch eine Verschiebung in Richtung der positiven bzw. negativen x-Achse erfolgen. Diese würde in einer Funktion dann wie folgt aussehen:
$g(x) = 2^{2-x}$
Eine weitere Art der Verschiebung bildet das Stellen einer weiteren Zahl in den Exponenten.
Teste dein neu erlerntes Wissen nun mit unseren Übungsaufgaben. Viel Erfolg dabei!
Weitere interessante Inhalte zum Thema
-
Funktionsuntersuchung von e-Funktionen und Scharen
Vielleicht ist für Sie auch das Thema Funktionsuntersuchung von e-Funktionen und Scharen aus unserem Online-Kurs Grundlagen der Analysis (Analysis 1) interessant.
-
Wertebereich
Vielleicht ist für Sie auch das Thema Wertebereich (Funktionsuntersuchung ganzrationaler Funktionen Teil 2) aus unserem Online-Kurs Grundlagen der Analysis (Analysis 1) interessant.