Wie berechnet man Achsenschnittpunkte von Funktionen?
In diesem Lerntext beschäftigen wir uns mit der Frage, wie man die Schnittpunkte von Funktionen mit den Achsen des Koordinatensystems berechnet.
Was sind Achsenabschnitte?
Funktionsgraphen werden in ein Koordinatensystem eingezeichnet. Dabei kann der Funktionsgraph die Koordinatenachse schneiden oder auch nur berühren. Die Schnittpunkte werden auch Achsenabschnitte genannt.
In diesem Lerntext erklären wir dir, wie die Schnittpunkte mit den Achsen berechnet werden.
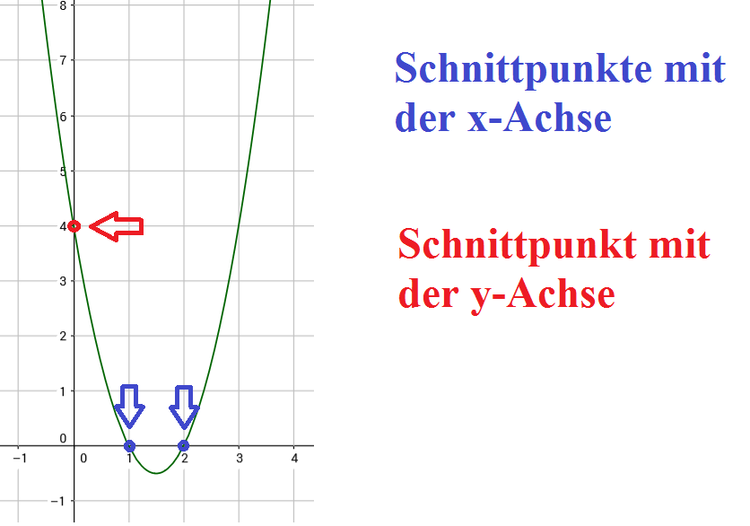
Die Abbildung oben zeigt eine Funktion, die zwei Schnittpunkte mit der x-Achse und einen Schnittpunkt mit der y-Achse hat. Die nachfolgende Abbildung zeigt, wie die Achsenabschnitte bezeichnet werden:
Hinweis
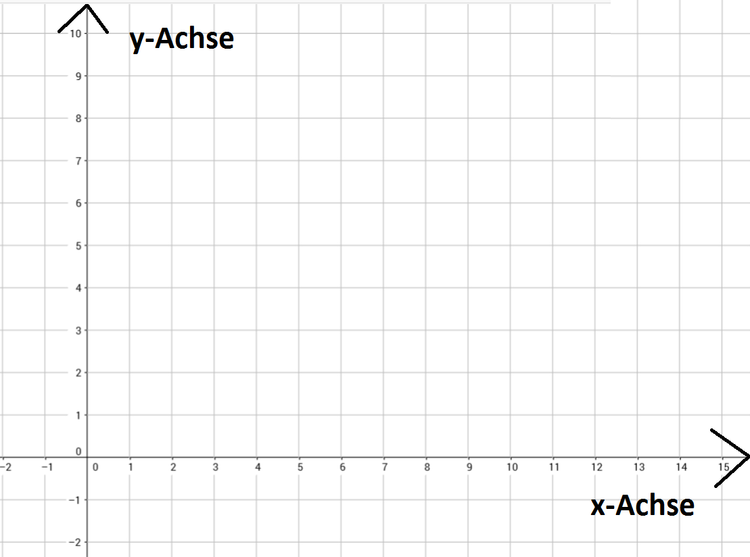
Wir sehen, dass die x-Achse von links nach rechts verläuft und die y-Achse von unten nach oben.
Schnittpunkte mit der x-Achse berechnen
Die Schnittpunkte mit der x-Achse werden auch Nullstellen genannt. Um diese zu ermitteln, muss die Funktion gleich null gesetzt werden. Anders gesagt muss der y-Wert den Wert null haben. Wenn wir uns das Koordinatensystem anschauen, ist dies logisch, da die x-Achse auf der Höhe von $y=0$ verläuft.
Methode
$f(x) = 0 \rightarrow$ Schnittpunkt(e) mit der x-Achse
Es gibt je nach Art der Funktion verschiedene Möglichkeiten die Nullstellen zu berechnen. Dazu gehört bei quadratischen Funktionen zum Beispiel die p-q-Fomel oder bei Funktionen mit $x^3$ die Polynomdivision.
Schnittpunkt mit der y-Achse berechnen
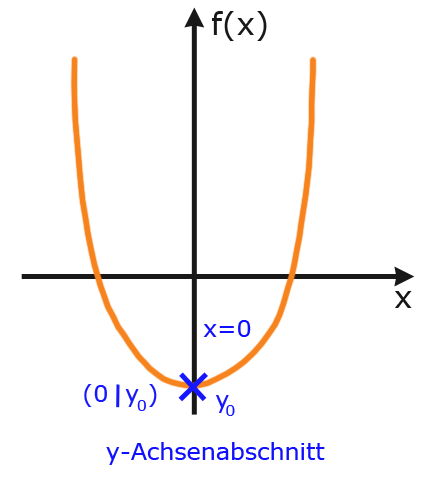
Der Schnittpunkt mit der y-Achse wird auch y-Achsenabschnitt genannt. Wichtig dabei ist, dass es nur einen einzigen Schnittpunkt geben kann. Dies liegt daran, dass jedem x-Wert einer Funktion nur maximal ein y-Wert zuordnet werden kann. Der x-Wert, an dem die Funktion die y-Achse schneidet, ist immer null.
Methode
$x=0 \rightarrow$ Schnittpunkt mit der y-Achse
Schnittpunkte mit den Koordinatenachsen bestimmen - Beispielaufgabe
Beispiel
Welche und vieviele Schnittpunkte hat die Funktion $f(x) = 2x^2+3x-1$ mit den Koordinatenachsen?
x-Achse
$f(x) = 0$
$f(x) = 2x^2+x-3 = 0$
Wir lösen die Gleichung mit der Mitternachtsformel
$x_1 =-1,5 $
$x_2 = 1$
$P_1(-1,5/0)$
$P_2(1/0)$
$~$
y-Achse
$x=0$
$f(0) = 2\cdot 0^2+0-3 = -3$
$f(0)=y =-3$
$P_3(0/-3)$
Die Funktion schneidet die x-Achse an den Punkten $P_1(-1,5/0)$, $P_2(1/0)$ und die y-Achse am Punkt $P_3(0/-3)$.
Mit den Übungsaufgaben kannst du nun dein Wissen überprüfen. Viel Erfolg dabei!
Video: Simon Wirth
Text: Chantal Rölle
Weitere interessante Inhalte zum Thema
-
y-Achsenabschnitt
Vielleicht ist für Sie auch das Thema y-Achsenabschnitt (Funktionsuntersuchung ganzrationaler Funktionen Teil 1) aus unserem Online-Kurs Grundlagen der Analysis (Analysis 1) interessant.
-
Schnittpunkte mit den Achsen
Vielleicht ist für Sie auch das Thema Schnittpunkte mit den Achsen (Funktionsuntersuchung ganzrationaler Funktionen Teil 1) aus unserem Online-Kurs Grundlagen der Analysis (Analysis 1) interessant.