Was ist eine Kurvendiskussion? - Erklärung
In diesem Lerntext beschäftigen wir uns mit der sogenannten Kurvendiskussion. Zu jeder beliebigen Funktion kann eine solche Kurvendiskussion durchgeführt werden. Die Ergebnisse der Kurvendiskussionen geben dann Informationen über den Verlauf und das Aussehen des Graphen.
Um eine Kurvendiskussion durchzuführen, müssen folgende Schritte der Reihe nach abgearbeitet werden:
7 Schritte der Kurvendiskussion - Überblick
Methode
- Definitionsmenge
- Schnittpunkte mit den Koordinatenachsen
- Symmetrieverhalten
- Verhalten im Unendlichen
- Monotonie und Extremwerte
- Krümmung und Wendepunkte
- Wertebereich und Graph
Die verschiedenen Schritte und auch die Reihenfolge kann je nach Schulbuch variieren. Wir schauen uns diese Schritte nun genauer an und erklären dir diese:
Kurvendiskussion durchführen - Schritt für Schritt
1. Definitionsmenge bestimmen
Die Definitionsmenge besteht aus allen Zahlen, die für die Variable $x$ eingesetzt werden dürfen.
Beispiel
$f(x) = x^2$
Welche Werte dürfen für $x$ eingesetzt werden? Es darf jede beliebige Zahl eingesetzt werden. $\rightarrow D_f= \mathbb{R} $
Der Definitionsbereich sind die reellen Zahlen.
Bei einem anderen Beispiel wird der Grund, wieso die Definitionsmenge bestimmt werden muss, deutlicher:
$g(x) = \sqrt{x}$
Wir wissen, dass unter der Wurzel keine negative Zahl stehen darf. Daher dürfen für $x$ nur positive Zahlen eingesetzt werden. Mathematisch formuliert bedeutet das : $D_f=\mathbb{R}^+$
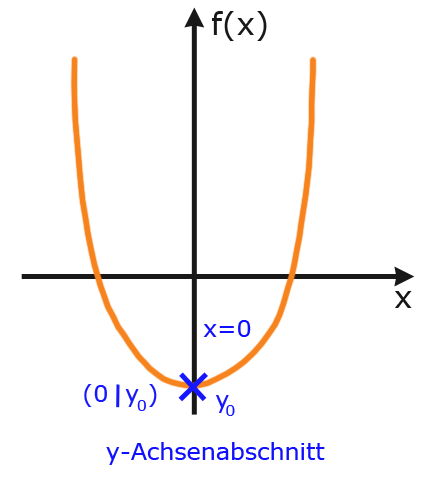
2. Schnittpunkte mit den Koordinatenachsen
Die Schnittpunkte mit den Koordinatenachsen sind zum einen die Nullstellen, die Schnittpunkte mit der x-Achse, und zum anderen der Schnittpunkt mit der y-Achse. Die Nullstellen berechnen wir, indem die Funktion gleich null gesetzt wird ($f(x) = 0$) und die Schnittpunkte mit der y-Achse, indem für die Variable null eingesetzt wird ($x =0$).
Beispiel
Was sind die Schnittpunkte der Funktion $f(x)=x^{2}-3x+2$ mit den Koordinatenachsen?
1. Nullstellen
$f(x) = 0$
$f(x)=x^{2}-3x+2=0$
Mit der pq-Formel erhalten wir:
$x_1 = 1~~~~\wedge~~~~x_2 = 2$
Die Funktion schneidet die x-Achse an den Stellen $x_1=1$ und $x_2=2$.
2. Schnittpunkte mit der y-Achse
$x=0$
$f(0)=0^{2}-30+2=2$
Die Funktion schneidet die y-Achse an der Stelle $y=2$.
3. Symmetrieverhalten bestimmen
Eine Funktion kann zur y-Achse symmetrisch sein oder auch zum Ursprung. Um zu überprüfen, ob die gegebene Funktion ein Symmetrieverhalten hat, muss folgendes gelten:
Merke
- $f(-x) = f(x)$: achsensymmetrisch
- $f(-x) = -f(x)$: punktsymmetrisch
Schauen wir uns dazu ein Beispiel an:
Beispiel
$f(x) = x^2$
Überprüfen wir, ob die Funktion achsensymmetrisch ist:
$f(-x) = f(x)\rightarrow (-x)^2 = x^2 ~~~~|\textcolor{red}{richtig}$
Ist die Funktion auch punktsymmetrisch?
$f(-x) = -f(x)\rightarrow x^2= - (x^2) ~~~~|\textcolor{red}{falsch}$
4. Verhalten im Unendlichen
Um das Verhalten im Unendlichen zu bestimmen, stellen wir uns die Funktion für eine sehr große und sehr kleine Variable vor.
Mathematisch wird dies dann so geschrieben: $\lim_{n \to \infty}x_n$ oder $\lim_{n \to -\infty}x_n$
Beispiel
Betrachten wir das gleiche Beispiel wie gerade: $f(x) = x^2$
Je größer $x$ wird, desto größer wird die Funktion. Das bedeutet, dass die Funktion für große x-Werte gegen unendlich läuft.
$\lim_{n \to \infty}x^2=\infty $
Je kleiner $x$ wird, desto größer wird der Funktionswert. Die Funktion verläuft auch für sehr kleine x-Werte ($-1000$) gegen positiv unendlich.
$\lim_{n \to -\infty}x^2=\infty $
5. Monotonie und Extremwerte bestimmen
Das Monotonieverhalten sagt etwas über die Steigung der Funktion aus. An den Extremstellen ändert sich das Steigungsverhalten entweder von steigend zu fallend oder von fallend zu steigend.
Um einen Extrempunkt zu bestimmen, müssen wir die erste Ableitung bilden und diese gleich null setzen.
Um zu bestimmen ob ein Hoch- oder Tiefpunkt vorliegt, bilden wir die zweite Ableitung und setzen den x-Wert ein:
Methode
Ist das Ergebis größer null liegt ein Tiefpunkt vor. Ist das Ergebnis kleiner null liegt ein Hochpunkt vor.
6. Krümmung und Wendepunkte bestimmen
Eine Funktion kann entweder links- oder rechtsgekrümmt sein. Der Wendepunkt ist der Punkt, an dem sich das Krümmungsverhalten ändert.
Um den Wendepunkt zu bestimmen, muss die zweite Ableitung gleich null gesetzt werden.
Methode
Wenn $f''(x) > 0$ ist, ist die Funktion linksgekrümmt.
Ist $f''(x) < 0$, ist die Funktion rechtsgekrümmt.
7. Wertebereich bestimmen und Graph skizzieren
Im letzten Schritt bestimmen wir den Wertebereich. Das bedeutet, dass wir die Werte bestimmen, die der Funktionswert annehmen kann. Dann können wir mit allen berechneten Punkten, den Graph skizzieren.
Nun hast du eine Übersicht über die Vorgehensweise einer Kurvendiskussion bekommen. Als kleine Hilfe stellen wir dir eine Übersichtsseite zum Herunterladen zur Verfügung. Hier kannst du dir eine Beispielaufgabe anschauen.
Außerdem kannst du dein Wissen ebenfalls mit unseren Übungsaufgaben testen. Viel Erfolg dabei!
Video: Fabian Serwitzki
Text: Chantal Rölle
Weitere interessante Inhalte zum Thema
-
Schnittpunkte mit den Achsen
Vielleicht ist für Sie auch das Thema Schnittpunkte mit den Achsen (Funktionsuntersuchung ganzrationaler Funktionen Teil 1) aus unserem Online-Kurs Grundlagen der Analysis (Analysis 1) interessant.
-
Kurvenschar Hochpunkt/Tiefpunkt
Vielleicht ist für Sie auch das Thema Kurvenschar Hochpunkt/Tiefpunkt (Funktionsuntersuchung ganzrationaler Kurvenscharen) aus unserem Online-Kurs Grundlagen der Analysis (Analysis 1) interessant.