Eine Umkehrfunktion bilden - Erklärung und Übung
In diesem Lerntext erklären wir dir, was eine Umkehrfunktion ist. Außerdem geben wir dir Beispiele, wie eine Umkehrfunktion gebildet werden kann und lösen Übungsaufgaben.
Was ist eine Umkehrfunktion? - Definition
Umkehrfunktionen ordnen, wie der Name schon sagt, eine Funktion umgekehrt zu. Das bedeutet, dass $x$-Wert und $y$-Wert vertauscht werden. Dies ist nur möglich, wenn es für jeden Funktionswert ($y$) nur einen $x$-Wert gibt. Die Umkehrfunktion der Funktion $f(x)$ wird mit $f^{\textcolor{red}{-1}} (x)$ gekennzeichnet. Die hochgestellte $\textcolor{red}{-1}$ ist das Zeichen für die Umkehrfunktion.
Methode
Eine Umkehrfunktion wird durch $f^{-1}(x)$ gekennzeichnet.
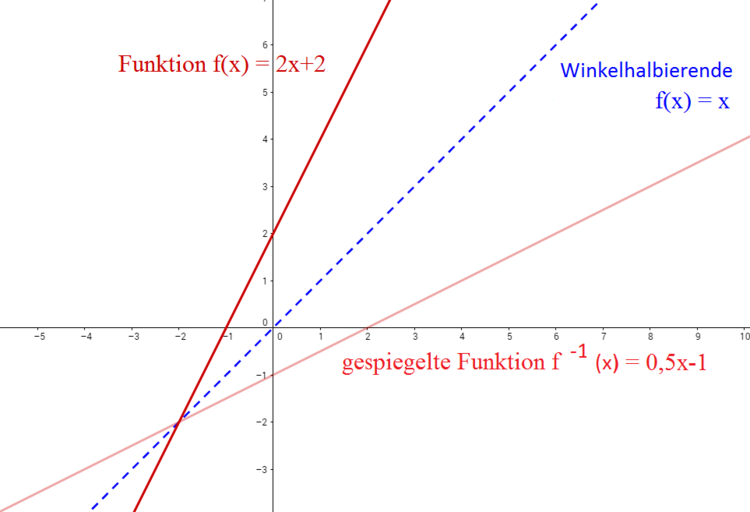
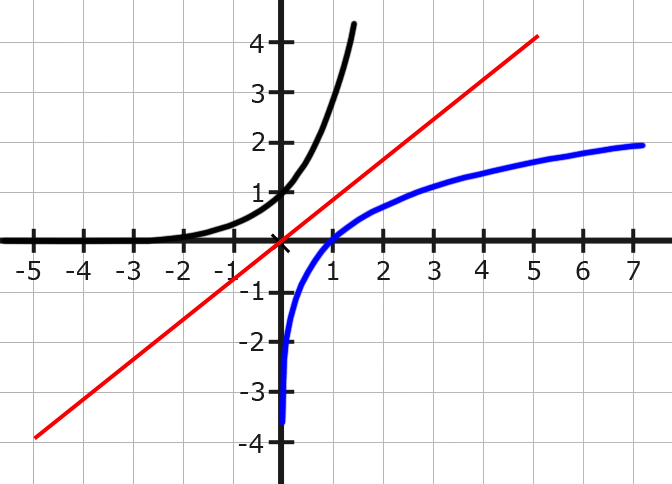
Wenn wir die Graphen einer Funktion und ihrer Umkehrfunktion betrachten, fällt auf, dass die Funktion an der Winkelhalbierenden gespiegelt wird. Die Winkelhalbierende wird beschrieben durch die Funktion $f(x)= x$.
Schauen wir uns jetzt an, wie die Umkehrfunktion von $f(x) = 2x+2$ gebildet wurde:
Eine Umkehrfunktion bilden - Schritt für Schritt
Um eine Umkehrfunktion zu bilden, muss die Funktion zunächst nach $x$ umgestellt werden. Danach werden $x$ und $y$ vertauscht, wobei sich auch die Definitions- und die Wertemenge vertauschen.
Methode
Vorgehensweise
- Die Funktion nach $x$ auflösen.
- $x$ und $y$ tauschen.
Schauen wir uns drei Beispiele an:
Beispiel
$f(x)=2x+2$
1. Die Funktion nach x auflösen.
$f(x) = y = 2x+2~~~~~~~~~|-2$
$y-2=2x~~~~~~~~~~~~~~|:2$
$\frac{y}{2}-1=x$
$= 0,5y-1=x$
2. $x$ und $y$ tauschen.
$y = 0,5x -1$ bzw. $f^{-1}(x) = 0,5x -1$
Beispiel
$f(x)=3x^2+5$
1. Die Funktion nach $x$ auflösen.
$f(x)= 3x^2+5~~~~~~~~~~~~|-5$
$\iff y-5 = 3x^2~~~~~~~~~~~~|:3$
$\iff \frac{y-5}{3}=x^2~~~~ ~~|\sqrt{~~}$
$\iff \sqrt{\frac{y-5}{3}}=x$
2. $x$ und $y$ tauschen.
$y = f^{-1}(x) = \sqrt{\frac{x-5}{3}} $
Beispiel
$f(x)=5x^3$
1. Die Funktion nach $x$ auflösen.
$f(x)=y =5x^3~~~~~~~~~~~~~|:5$
$\iff \frac{y~}{5~}=x^3~~~~~~~~~~~~~~~~~~~~~~~~~~~|\sqrt[3]{~~}$
$\iff \sqrt[3]{\frac{y~}{5~}}=x$
2. $x$ und $y$ tauschen.
$f^{-1}(x) = y= \sqrt[3~]{\frac{x~}{5~}}$
Umkehrfunktion bilden - Anwendung im Alltag
Wann muss eine Umkehrfunktion gebildet werden? Es gibt nur wenige Anwendungsbeispiele.
Ein Beispiel aus der Wirtschaft: Normalerweise wird die Nachfrage nach einem Produkt in Abhängigkeit des Preises abgebildet. Man kann jedoch auch den Preis in Abhängigkeit der Nachfrage darstellen. Dies könnte einen Hersteller interessieren, der eine bestimmte Menge eines Produktes verkaufen möchte und wissen möchte, welchen Preis er pro Einheit verlangen sollte, um alle produzierten Einheiten zu verkaufen.
Mit den Übungsaufgaben kannst du dein neu erworbenes Wissen überprüfen. Dabei wünschen wir dir viel Spaß und Erfolg!
Weitere interessante Inhalte zum Thema
-
Logarithmusfunktionen
Vielleicht ist für Sie auch das Thema Logarithmusfunktionen (Funktionsklassen) aus unserem Online-Kurs Weiterführende Aufgaben der Analysis (Analysis 2) interessant.
-
Steckbriefaufgaben
Vielleicht ist für Sie auch das Thema Steckbriefaufgaben (Differentialrechnung) aus unserem Online-Kurs Weiterführende Aufgaben der Analysis (Analysis 2) interessant.