Potenzfunktionen - Monotonie bestimmen
In diesem Lerntext beschäftigen wir uns mit den verschiedenen Monotoniearten von Potenzfunktionen.
Es gibt verschiedene Arten von Potenzfunktionen, deren Monotonieverhalten sich unterscheidet. Daher schauen wir uns in diesem Text die Monotonie von Potenzfunktionen genau an.
Was sind Potenzfunktionen? - Wiederholung
Merke
Potenzfunktionen sind Funktionen, die mindestens eine Variable $x$ mit einem Exponenten $n \neq 0$ besitzen und deren Streckungsfaktor $a \neq 0$ ist. Die allgemeine Schreibweise ist: $f(x) = a\cdot x^{n}$.
Hierbei werden die Funktionen, abhängig vom Exponenten, in vier verschiedene Fälle unterteilt:
Hinweis
- gerader, positiver Exponent
- gerader negativer Exponent
- ungerader, positiver Exponent
- ungerader negativer Exponent
Was Monotonie bedeutet und wie sie von jeder beliebigen Funktion bestimmt werden kann, erfährst du hier: Monotonie
Monotonie von Potenzfunktionen
Im Folgenden schauen wir uns das Monotonieverhalten für eine Potenzfunktion mit geradem und positivem Exponenten an:
gerader positiver Exponent
Beispiel
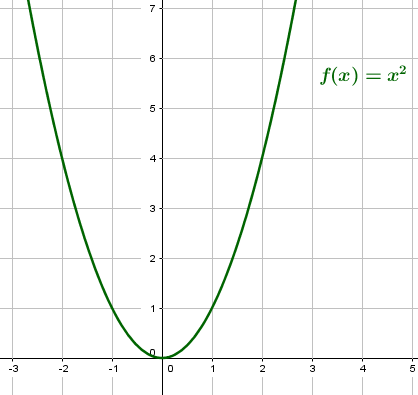
Ein Beispiel für diese Art von Potenzfunktionen ist: $f(x) = x^2$
Wir sehen, dass die Funktion im Punkt $P(0/0)$ einen Tiefpunkt hat. Jede Potenzfunktion mit geraden, positiven Exponenten besitzt im gleichen Punkt einen Tiefpunkt. Vor dem Tiefpunkt ist die Funktion streng monoton fallend und nach dem Tiefpunkt streng monoton steigend.
Merke
Die Normalparabel ist weder monoton fallend noch monoton steigend.
Beschränkt man sich jedoch auf die Intervalle:
$x≤0$, so verläuft die Parabel dort streng monoton fallend
$x>0$, so verläuft die Parabel dort streng monoton steigend.
gerader negativer Exponent
Nun schauen wir uns das Monotonieverhalten für eine Potenzfunktion mit geradem und negativem Exponenten an:
Beispiel
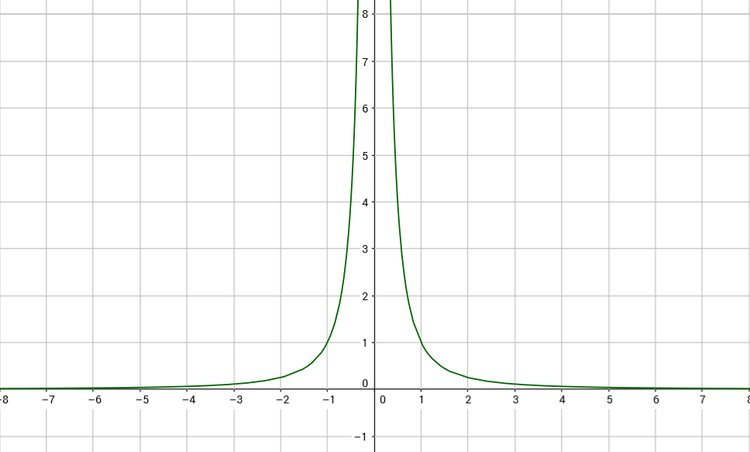
Ein Beispiel für eine Potenzfunktion mit geradem, negativem Exponenten ist: $f(x) = x^{-4}$
Die Funktion hat keinen Hoch- oder Tiefpunkt. Je näher der x-Wert an Null kommt, desto größer wird der y-Wert. In der Abbildung können wir sehen, dass die Funktion für alle x-Werte kleiner Null, streng monoton steigend ist und für alle Werte größer Null streng monoton fallend ist.
Merke
Die Funktion ist weder monoton fallend noch monoton steigend.
Beschränkt man sich jedoch auf die Intervalle:
$x<0$, so verläuft die Funktion dort streng monoton steigend
$x>0$, so verläuft die Funktion dort streng monoton fallend.
Beachte: Für $x=0$ ist die Funktion nicht definiert!
ungerader positiver Exponent
Das Monotonieverhalten für eine Potenzfunktion mit ungeradem und positivem Exponenten schauen wir uns jetzt an:
Beispiel
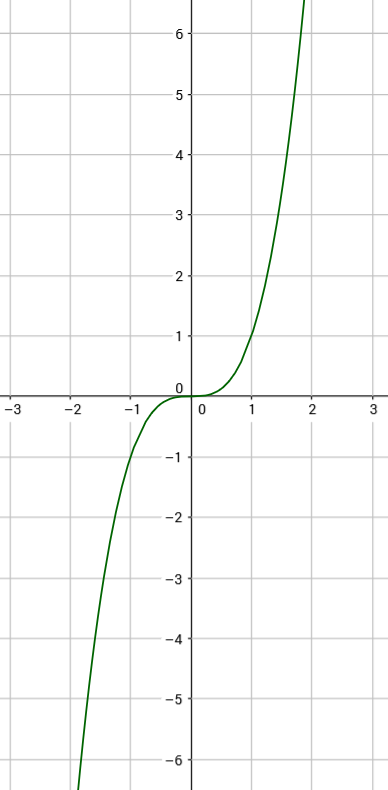
Ein Beispiel für eine Potenzfunktion mit ungeradem, positivem Exponent ist: $f(x) = x^{3}$
Funktionen mit ungeraden, positiven Exponenten haben am Punkt $P(0/0)$ einen Sattelpunkt. An dieser Stelle ist die Steigung gleich Null. Dennoch ist jeder x-Wert beliebig größer als sein Vorgänger.
Wir sehen, dass die Funktion in jedem Punkt steigt.
Merke
Für alle $x$ gilt $\rightarrow$ streng monoton steigend.
ungerader negativer Exponent
Im Folgenden schauen wir uns das Monotonieverhalten für eine Potenzfunktion mit ungeradem und negativem Exponenten an:
Beispiel
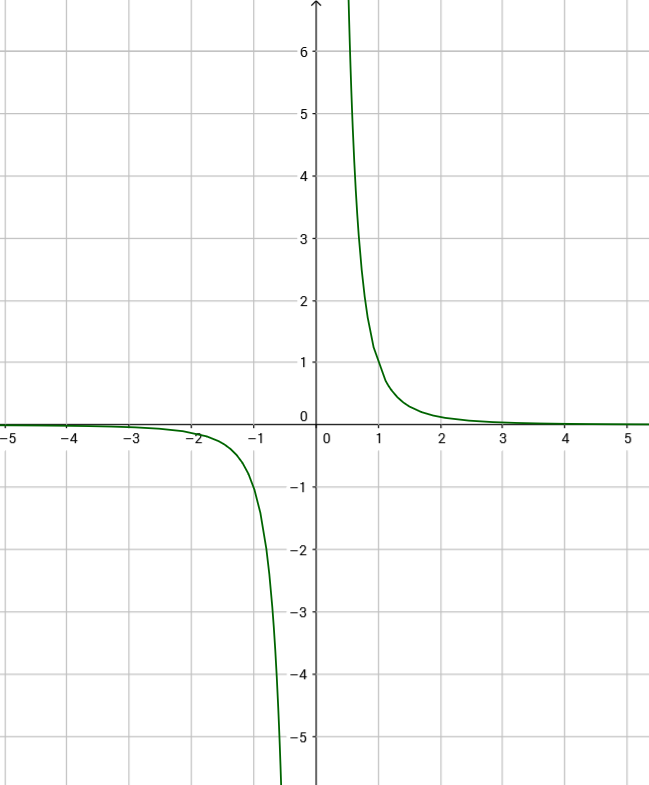
Ein Beispiel für eine Potenzfunktion mit ungeraden, negativen Exponent ist: $f(x) = x^{-3}$
Je näher der x-Wert von links an Null kommt, desto kleiner wird der y-Wert. Je näher der x-Wert von rechts ins Unendliche läuft, desto kleiner wird der y-Wert. In der Abbildung können wir sehen, dass die Funktion für beide Fälle streng monoton fallend ist.
Merke
Betrachtung der Intervalle:
$x<0$, so verläuft die Funktion dort streng monoton fallend
$x>0$, so verläuft die Funktion dort auch streng monoton fallend.
Beachte: Für $x=0$ ist die Funktion nicht definiert!
Nun weißt du, was das Monotonieverhalten von Potenzfunktionen ist. Mit den Übungsaufgaben kannst du dein Wissen testen. Viel Erfolg dabei!
Video: Simon Wirth
Text: Chantal Rölle
Weitere interessante Inhalte zum Thema
-
Globalverhalten, Wertebereich, Monotonie kubische Schar
Vielleicht ist für Sie auch das Thema Globalverhalten, Wertebereich, Monotonie kubische Schar (Funktionsuntersuchung ganzrationaler Kurvenscharen) aus unserem Online-Kurs Grundlagen der Analysis (Analysis 1) interessant.
-
Potenzregel
Vielleicht ist für Sie auch das Thema Potenzregel (Ableiten) aus unserem Online-Kurs Grundlagen der Analysis (Analysis 1) interessant.