Normalparabel verschieben - Wie geht das?
Der Graph der Funktion $f(x)=x^2$ wird Normalparabel genannt. Der Graph dieser Funktion kann in einem Koordinatensystem in 4 verschiedene Richtungen verschoben werden: Nach oben, nach unten, nach links und nach rechts.
Normalparabel verschieben - Eine Übersicht
Merke
Verschiebung in Richtung der y-Achse
- nach $\textcolor{red}{oben}$ : $f(x) = x^2 \textcolor{red}{+ a} \rightarrow$ Verschiebung des Graphen um a nach oben
- nach $\textcolor{red}{unten} $ : $f(x) = x^2 \textcolor{red}{-b} \rightarrow$ Verschiebung des Graphen um b nach unten
Verschiebung in Richtung der x-Achse
- nach $\textcolor{red}{rechts} $ : $f(x) = (x \textcolor{red}{-c})^2 \rightarrow$ Verschiebung des Graphen um c nach rechts
- nach $\textcolor{red}{links} $ : $f(x) = (x \textcolor{red}{+d})^2 \rightarrow$ Verschiebung des Graphen um d nach links
Verschiebung in Richtung der y-Achse
Verschiebung nach oben
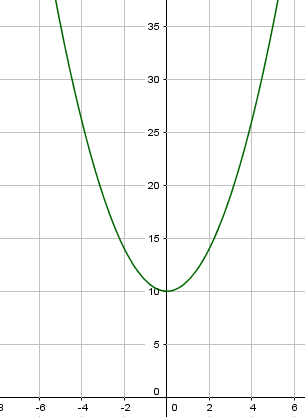
Die Normalparabel wird nach oben verschoben, indem du an die Funktionsgleichung $f(x) = x^2$ einen positiven Wert hinzu addierst. Also zum Beispiel $f(x) = x^2+10$. Dann wird der Graph um 10 Einheiten nach oben verschoben.
Die Normalparabel wurde um $10$ Einheiten in Richtung der y-Achse nach oben verschoben.
Verschiebung nach unten
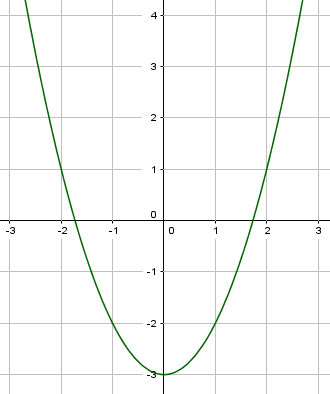
Die Normalparabel wird nach unten verschoben, indem du an die Funktionsgleichung $f(x) = x^2$ einen negativen Wert hinzu addierst. Also zum Beispiel $f(x) = x^2-3$.
Die Normalparabel wurde um $3$ Einheiten in Richtung der y-Achse nach unten verschoben.
Verschiebung in Richtung der x-Achse
Verschiebung nach rechts
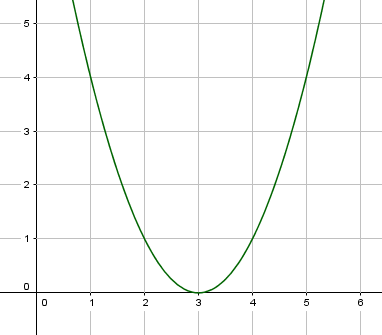
Der Graph der Normalparabel wird nach rechts verschoben, indem von dem $x$, das quadriert wird, ein bestimmter Wert subtrahiert wird. Diese Zahl steht mit dem $x$ zusammen in der Klammer.
Also zum Beispiel $f(x) = (x-3)^2$.
Also bewirkt der negative Wert, der mit dem $x$ in der Klammer steht, dass die Parabel auf der x-Achse nach rechts, also in den positiven Bereich verschoben wird.
Merke dir einfach: Wenn in der Klammer ein Minus steht, wird der Graph nach rechts, also in den positiven Bereich, verschoben.
Verschiebung nach links
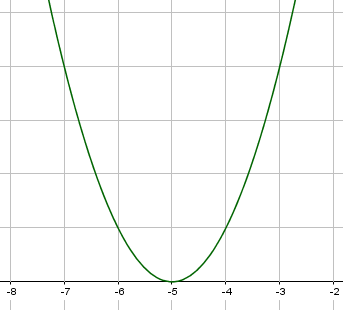
Hier ist es genau umgekehrt im Vergleich zur Verschiebung nach rechts: Der Wert in der Klammer ist nun positiv und der Graph der Parabel wird daher nach links, also in den negativen Bereich, verschoben. Hierzu ein Beispiel: $f(x) = (x+5)^2$
Also bewirkt der positive Wert, der mit dem $x$ in der Klammer steht, dass die Parabel auf der x-Achse nach links, also in den negativen Bereich verschoben wird.
Merke dir einfach: Wenn in der Klammer ein Plus steht, wird der Graph nach links, also in den negativen Bereich, verschoben.
Normalparabel in zwei Richtungen verschieben - Beispiel mit Lösung
Natürlich können wir den Graphen zum Beispiel auch nach unten und gleichzeitig nach rechts verschieben.
Sagen wir der Graph soll um $3$ nach unten und um $1$ nach rechts verschoben werden. Wie muss unsere Funktion dann aussehen?
Vertiefung
Lösung
Wir gehen schrittweise vor:
Zuerst verschieben wir den Graphen um $3$ nach unten $\rightarrow f(x) = x^2-3$.
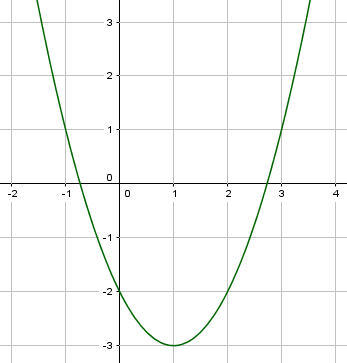
Dann noch um $1$ nach rechts $\rightarrow f(x) = (x-1)^2-3$.
Jetzt haben wir unseren Graphen und der sieht gezeichnet so aus:
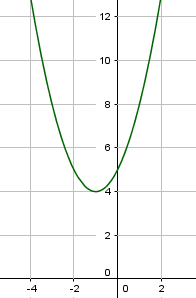
Die Funktion kann auch in Normalform angegeben werden. Leider können wir daraus die Verschiebung nicht direkt ablesen. Schauen wir uns ein Beispiel an. $f(x) = x^2+2x+5$. Der Graph dazu sieht so aus:
Das einzige, was wir aus der Funktion direkt ablesen können, ist der y-Achsenabschnitt, also hier $5$.
Nun können wir die Form natürlich in die Scheitelpunktform umformen.
$f(x) = x^2+2x+5$
$f(x) = (x^2+2x+1-1)+5$
$f(x) = (x^2+2x+1)+5-1$
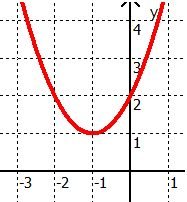
$f(x) = (x+1)^2+4$
Jetzt können wir die Verschiebung ablesen. Der Graph wird um 1 nach links verschoben und um 4 nach oben. Wir können dies nun nochmal mit dem Bild von oben vergleichen; das Bild bestätigt, dass der Scheitelpunkt der Funktion bei S(-1/4) liegt.
Jetzt hast du einen Überblick über die verschiedenen Verschiebungen der Normalparabel bekommen. Dieses Wissen kannst du gerne an unseren Übungen testen. Wir wünschen dir viel Spaß dabei!
Weitere interessante Inhalte zum Thema
-
Quadratische Funktionen mit pq-Formel und Mitternachtsformel lösen
Vielleicht ist für Sie auch das Thema Quadratische Funktionen mit pq-Formel und Mitternachtsformel lösen (Gleichungen lösen) aus unserem Online-Kurs Vorkenntnisse zur Analysis interessant.
-
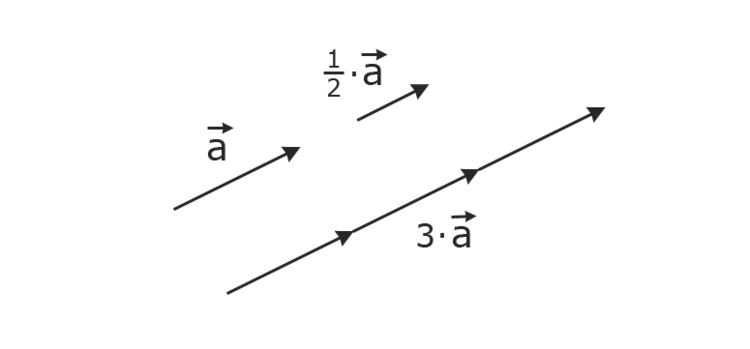
Vielfache von Vektoren bilden
Vielleicht ist für Sie auch das Thema Vielfache von Vektoren bilden (Rechnen mit Vektoren) aus unserem Online-Kurs Analytische Geometrie / Lineare Algebra (Agla) interessant.