Mitternachtsformel - Nullstellen von Funktionen berechnen

Es gibt verschiedene Möglichkeiten, um die Nullstellen einer quadratischen Funktion zu bestimmen. Eine davon ist die Mitternachtsformel - Sie wird auch abc-Formel genannt.

Was ist die Mitternachtsformel? - Definition

Wir müssen, wie bei der p-q-Formel auch, für die Mitternachtsformel Werte ablesen und diese dann in die Formel einsetzen und ausrechnen. Wie dir wahrscheinlich auffällt, ähnelt die Mitternachtsformel der p-q-Formel sehr stark. Sie leitet sich sogar daraus ab.

Wir schauen uns zunächst ein Beispiel an:

Mitternachtsformel und p-q-Formel - Unterschied

Hätten wir diese Gleichung von oben mit der p-q-Formel bearbeitet, so hätten wir am Anfang alles durch 0,25 teilen müssen und wären dann auf das gleiche Ergebnis gekommen.

Du kannst dir selbst aussuchen, welche Form dir besser liegt.
Die Mitternachtsformel ist in der Hinsicht einfacher, dass nicht so viele kleine Brüche entstehen können. Bei der p-q-Formel teilst du durch den Faktor vor dem $x^2$, dadurch entstehen teilweise kleine Brüche. Dies vermeidest du indem du die abc-Formel anwendest.
Dabei entstehen beim Einsetzen und Ausrechnen jedoch schneller Fehler, da die abc-Formel etwas komplizierter ist.
Am Besten probierst du beide Formeln einmal aus und entscheidest dann, mit welcher du besser rechnen kannst.

Nullstellen mit der Mitternachtsformel berechnen - Beispiel

Die Funktion $f(x) = 0,5(x-4)^2-2$ ist gegeben und die Nullstellen sollen bestimmt werden.

Zunächst müssen wir die Formel sowohl für die Mitternachtsformel als auch für die p-q-Formel umformen. Die Gleichung ist in der Scheitelpunktform angegeben, aber wir benötigen die Normalform um $a,b$ und $c$ oder auch $p$ und $q$ ablesen zu können.

Umformung der Scheitelpunktform in die Normalform
$f(x) = 0,5(x-4)^2-2$
$f(x) = 0,5(x^2+2\cdot x\cdot(-4)+4^2)-2$
$f(x) = 0,5(x^2-8\cdot x+16)-2$
$f(x) = 0,5\cdot x^2-0,5\cdot8\cdot x+0,5\cdot16-2$
$f(x) = 0,5\cdot x^2-4\cdot x+8-2$
$f(x) = 0,5\cdot x^2-4\cdot x+6$

Nun haben wir unsere Normalform gegeben und können hiermit weiter rechnen.

Berechnung der Nullstellen mit der Mitternachtsformel
$f(x) = 0,5\cdot x^2-4\cdot x+6$

Wir lesen zuerst $a, b$ und $c$ ab.
$a= 0,5$
$b= -4$
$c= 6$

Jetzt setzen wir die Werte in die Formel ein.
$x_{1,2} = \frac{{-b}~\pm~\sqrt{{b}^2~-~4~ \cdot~{a} \cdot~{c}}}{2~ \cdot~{a}}$

$x_{1,2} = \frac{{-(-4)}~\pm~\sqrt{{(-4)}^2~-~4~ \cdot~{0,5} \cdot~{6}}}{2~ \cdot~{0,5}}$

$x_{1,2} = \frac{4~\pm~\sqrt{16~-12}}{1}$

$x_{1,2} = {4}~\pm~\sqrt{4}$

$x_{1,2} = {4}~\pm~2$

$x_1 = 4+2=6$

$x_2 = 4-2=2$

Also sind unsere zwei Nullstellen $2$ und $6$.

Berechnung der Nullstellen mit der p-q-Formel
$f(x) = 0,5\cdot x^2-4\cdot x+6$

Zuerst müssen wir durch den Faktor, der vor dem $x^2$ steht teilen.
$f(x) = 0,5\cdot x^2-4\cdot x+6$             $|:0,5$
$f(x) = x^2-8\cdot x+12$

Nun können wir $p$ und $q$ ablesen.
$p= -8$
$q= 12$

Jetzt setzen wir die Werte in die Formel ein.
$x_{1/2} = -\frac{p}{2}\pm \sqrt{(\frac{p}{2})^2-{q}}$
$x_{1/2} = -\frac{(-8)}{2}\pm \sqrt{(\frac{(-8)}{2})^2-{12}}$
$x_{1/2} = 4\pm \sqrt{\frac{64}{4}-12}$
$x_{1/2} = 4\pm \sqrt{16-12}$
$x_{1/2} = 4\pm \sqrt{4}$
$x_{1/2} = 4\pm 2$
$x_1 = 4 +2=6$
$x_2 = 4- 2=2$

Und natürlich sind die Nullstellen die gleichen $\rightarrow 2, 6$

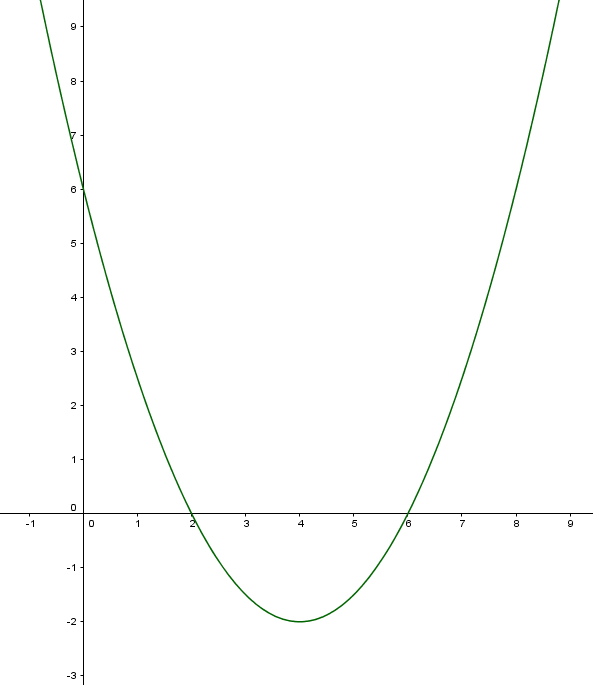
Die Funktion sieht dann folgendermaßen aus:

Abbildung der Funktion: $f(x) = 0.5 x^2 - 4x + 6 $

Wir können die zwei Nullstellen ($2$ und $6$) ablesen. Außerdem den Scheitelpunkt, der bei $S(4/-2)$ liegt  und auch den y-Achsen-Abschnitt, der bei $y=6$ ist. 

Jetzt kannst du Nullstellen mit der Mitternachtsformel und auch mit der pq-Formel errechnen. Teste dein neues Wissen mit unseren Übungen!