Anleitung: Wie zeichnet man quadratische Funktionen?
Quadratische Funktionen begegnen dir öfter als du glaubst. Wir schauen uns hier zunächst einmal an, was eine quadratische Funktion ist, um sie dann zeichnen zu können.
Quadratische Funktion - Definition
Bei quadratischen Funktionen bzw. Gleichungen wird das x zum Quadrat genommen. Daher heißen sie auch quadratische Funktionen. Aus dem gleichen Grund gibt es zu jeden y-Wert zwei x-Werte! Hat man z.b den y-wert 4 kann man diesem x=2 und x=-2 zuordnen.
Quadratsiche Funktionen im Alltag
Auch im Alltag begegnen dir einige quadratische Funktionen. Zum Beispiel haben die meisten Brücken die Form einer Parabel.
Hinweis
Parabel ist eigentlich nur ein anderes Wort für die typische Form einer quadratischen Funktion, welche du noch näher kennenlernen wirst.
Die Änderung der Temperatur im Verlauf des Tages, erinnert an den Verlauf einer quadratischen Funktion. Wenn du die Abhängigkeit von Temperatur zur Zeit in ein Koordinatensystem einzeichnen würdest, würde die Funktion der Form einer Parabel ähneln. Am Anfang des Tages ist sie am niedrigsten, dann steigt sie bis zur Mittagszeit auf ihren Hochpunkt und sinkt danach wieder bis zur niedrigsten Temperatur.
Schritt für Schritt - Wie zeichnet man eine quadratische Funktion?
Anlegen einer Wertetabelle
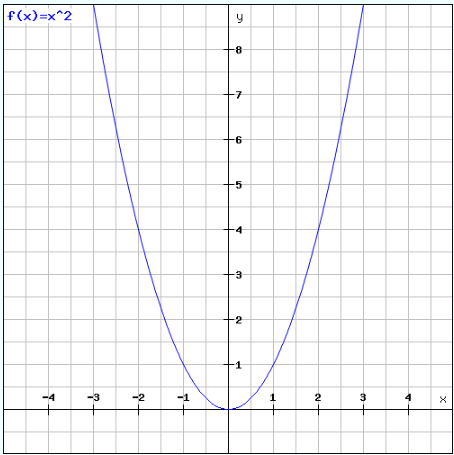
Erst einmal schauen wir uns den Graph von der Funktion $f(x) = x^2$ an. Dazu können wir eine Wertetabelle erstellen. Wir setzen in die Funktion beliebige x-Werte ein und erhalten durch ausrechnen den y-Wert.
| x-Werte | y-Werte |
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
Punkte ins Koordinatensystem eintragen
Nun haben wir schon 8 Punkte, die wir in unser Koordinatensystem einzeichnen können. Für die negativen x-Werte, also -1, -2, -3, -4 ,können wir nämlich die gleichen Zahlen, wie für die positiven x-Werte, einsetzen. Da $-1\cdot(-1) = 1$ ist, genauso ist es mit $-2\cdot(-2) = 4$ und so weiter. Also haben die positiven und negativen x-Wert, bei einer quadratischen Gleichung, immer den gleichen positiven y-Wert. Und genau das macht unsere quadratische Gleichung aus.
Graph zeichnen
Versuche nun einmal den Graph selber zu zeichnen, indem du die Punkte miteinander verbindest. Schaue dir dann die Abbildung an und vergleiche sie mit deiner Zeichnung.
Abbildung der Funktion
Eine quadratische Funktion zeichnen - Beispielaufgabe
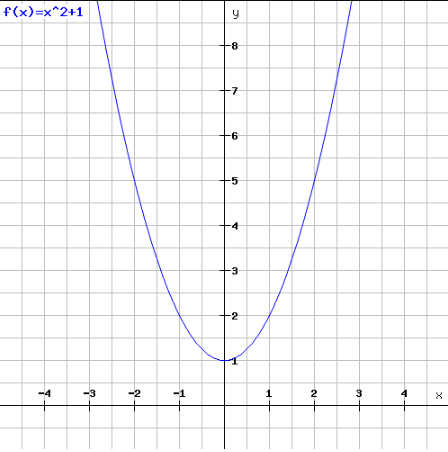
Ein anderes Beispiel mit einer kleinen Veränderung ist die Funktion $f(x) = x^2+1$. Zuerst machen wir wieder unsere Wertetabelle.
| x-Werte | y-Werte |
| 1 | 2 |
| 2 | 5 |
| 3 | 10 |
| 4 | 17 |
Aus der Tabelle können wir wieder Punkte entnehmen und die in unser Koordinatensystem einzeichnen. Und genau wie eben kann für den negativen x-Wert der gleiche Wert von y eingezeichnet werden. Daher ist es beim Einzeichnen hilfreich, zuerst den positiven und dann direkt den negativen Wert einzuzeichnen. Somit musst du nicht zweimal nach dem y-Wert suchen.
Zeichne nun die Funktion selber oder überlege was mit deiner Funktion $f(x) = x^2$ passiert.
Abbildung der verschobenen Funktion
Wie du siehst, wurde unsere Funktion von eben ($f(x) = x^2$) um 1 Einheit nach oben verschoben.
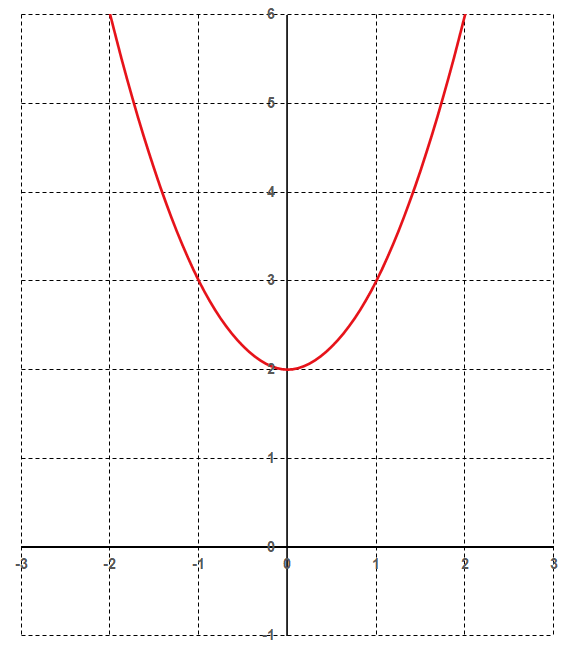
In der Gleichung wird die Verschiebung nach oben oder unten von der Normalparabel ($x^2$) durch ein plus oder minus hinter dem $x^2$ angedeutet. So gibt es zum Beispiel auch die Funktion $f(x) = x^2+99$ bei der die Normalparabel um 99 Einheiten nach oben verschoben wird.
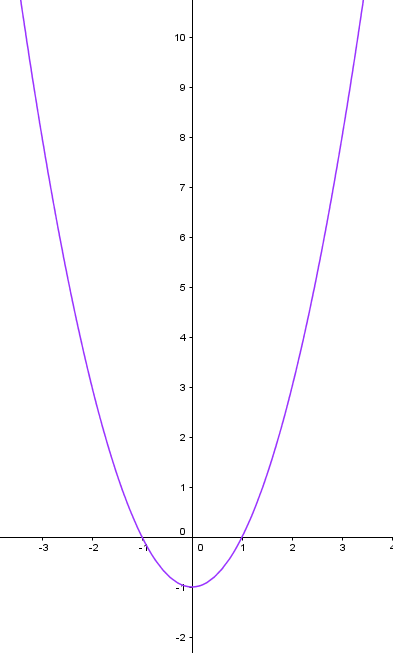
Es geht auch anders herum. Eine Funktion kann auch nach unten verschoben werden. Ein einfaches Beispiel ist $f(x) = x^2-1$. Dann wir der Graph um 1 Einheit nach unten verschoben und sieht dann so aus:
Dabei entstehen, wie du wahrscheinlich schon siehst, Nullstellen.Das sind die Schnittpunkte der Parabel mit der x-Achse. Bei dem oberen Graphen sind die Punkte $A(0/-1)$ und $B(0/1)$ Nullstellen, dazu kommen wir aber später nochmal.
Merke
So jetzt weißt du, was eine quadratische Funktion ist und wie du sie zeichnen kannst. Ein wesentlicher Unterschied zur linearen Funktion ist, dass du für jeden y-Wert zwei x-Werte erhältst.
Teste dein neu erlerntes Wissen mit unseren Übungsaufgaben. Wir wünschen dabei viel Spaß!
Weitere interessante Inhalte zum Thema
-
Quadratische Funktion durch Ausklammern lösen
Vielleicht ist für Sie auch das Thema Quadratische Funktion durch Ausklammern lösen (Gleichungen lösen) aus unserem Online-Kurs Vorkenntnisse zur Analysis interessant.
-
Quadratische Funktionen lösen
Vielleicht ist für Sie auch das Thema Quadratische Funktionen lösen (Gleichungen lösen) aus unserem Online-Kurs Vorkenntnisse zur Analysis interessant.