Kosinusfunktion - die Eigenschaften ganz einfach erklärt
In diesem Lerntext erhältst du einen Überblick über die Eigenschaften der Kosinusfunktion. Außerdem erklären wir dir, wie du die Kosinuskurve in x- oder y-Richtung verschieben kannst.
Kosinusfunktion - Wie lautet die allgemeine Funktionsgleichung?
Die Kosinusfunktion ist eine der trigonometrischen Funktionen und ordnet jedem $x$ seinen entsprechenden Kosinuswert $y$ zu.
Merke
$y~= cos(x)$
Eigenschaften der Kosinusfunktion - Überblick
Ähnlich wie die Sinusfunktion besitzt die Kosinusfunktion einige Besonderheiten. Für die Skalierung der x-Achse nutzt man auf Grund des geometrischen Hintergrunds das Bogenmaß. Die Kurve der Kosinusfunktion verläuft periodisch.
Kosinusfunktion - Definitions- und Wertemenge
Für die x-Werte der Kosinusfunktion sind alle reellen Zahlen erlaubt. Die Definitionsmenge lautet also:
$\mathbb{D} = \mathbb{R}$
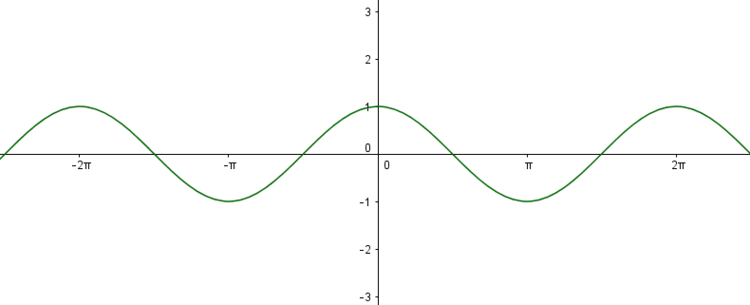
Wie du in der Abbildung erkennen kannst, können die y-Werte nur Werte zwischen $-1$ und $1$ annehmen. Der Wertebreich der normalen Kosinusfunktion lautet also:
$W= [-1;1]$
Kosinuskurve - Periode und Symmetrieverhalten
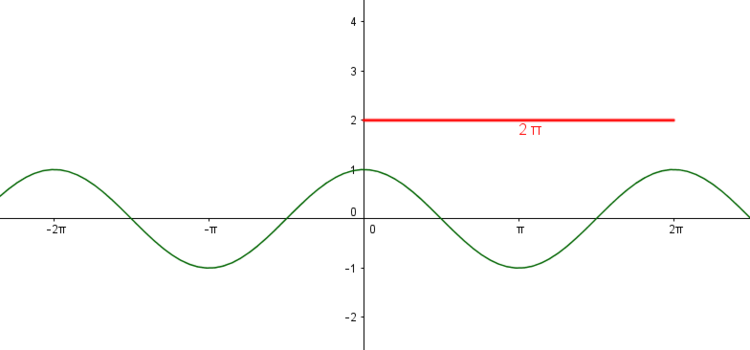
Die Kosinuskurve verläuft periodisch, das heißt, dass sich ein einzelner Abschnitt immer wieder wiederholt. Man kann auch sagen, dass sich die Funktionwerte ($y$) im selben Abstand wiederholen. Eine Wellenbewegung oberhalb und unterhalb der x-Achse enspricht einer Periode von $2 \pi$.
Außerdem ist die Kosinusfunktion achsensymmetrisch zur y-Achse. Dies lässt sich rechnerisch folgendermaßen beweisen:
$cos(-x) = cos (x)$
Wenn du nicht mehr genau weißt, wie du die Symmetrie einer Funktion rechnerisch beweisen kannst, findest du in unserem Lerntext zu Kurvendiskussionen eine ausführliche Erklärung.
Kosinusfunktion - Die Nullstellen
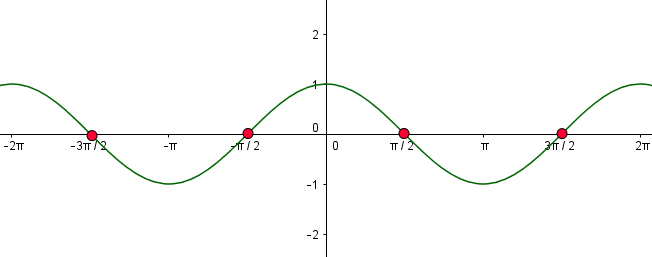
Aufgrund ihres periodischen Verlaufs entlang der x-Achse, besitzt die Kosinusfunktion unendlich viele Nullstellen, die jeweils um den Wert $\pi$ auseinander liegen.
Merke
Für die Berechnung der Nullstellen der Kosinusfunktion gilt:
$x_k = \frac{\pi}{2} + k \cdot \pi $
Dabei können für $k$ alle möglichen ganzen Zahlen eingesetzt werden.
Beispiel
$x_{-1} = \frac{\pi}{2} + (-1) \cdot \pi = - \frac{\pi}{2}$
$x_{0} = \frac{\pi}{2} + (0) \cdot \pi = \frac{\pi}{2}$
$x_{2} = \frac{\pi}{2} + (2) \cdot \pi = \frac{3 \cdot \pi}{2}$
Kosinusfunktion - Relative Maxima und Minima
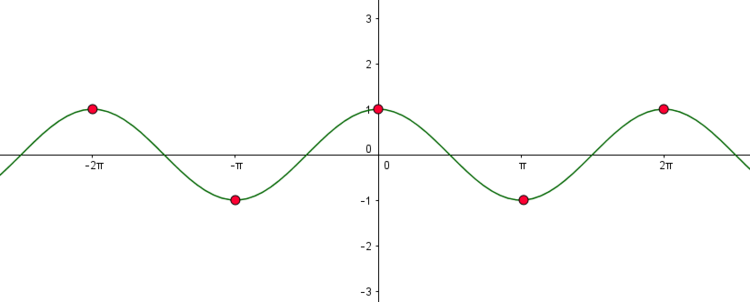
Auch für die Extremwerte (Hoch- und Tiefpunkte) lässt sich aufgrund des periodischen Verlaufs der Kosinuskurve eine allgemeine Formel angeben.
Merke
Relative Maxima
$x_k = k \cdot 2 \cdot \pi$
Beispiel
$x_{-1} = -1 \cdot 2 \cdot \pi = -2 \cdot \pi$
$x_1 = 1 \cdot 2 \cdot \pi = 2 \cdot \pi$
Merke
Relative Minima
$x_k = \pi + k \cdot 2 \cdot \pi$
Beispiel
$x_{-1} = \pi + k \cdot 2 \cdot \pi = \pi + (-1) \cdot 2 \cdot \pi = - \pi$
$x_{1} = \pi + 1 \cdot 2 \cdot \pi = 3 \cdot \pi$
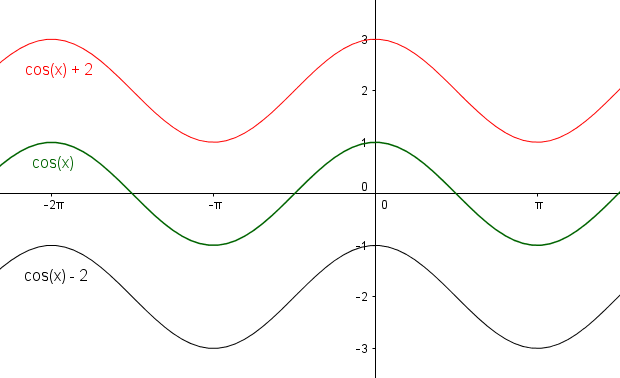
Kosinusfunktion - Verschiebung in y-Richtung
Die Kosinusfunktion wird entlang der y-Achse verschoben, wenn ein Wert zum Funktionsterm dazu addiert oder davon abgezogen wird. Dadurch wird die Kosinuskurve entlang der y-Achse in positive oder negative Richtung verschoben.
Merke
$y = cos(x) + d$
Der Paramteter $d$ verschiebt die Kosinuskurve entlang der y-Achse.
$d>0 \rightarrow$ Verschiebung nach oben
Bei der Verschiebung in y-Richtung ist zu beachten, dass die verschobenen Kosinuskurven keine Nullstellen, also keine Schnittpunkte mit der x-Achse, besitzen. Die x-Koordinaten der Maxima und Minima ändern sich nicht.
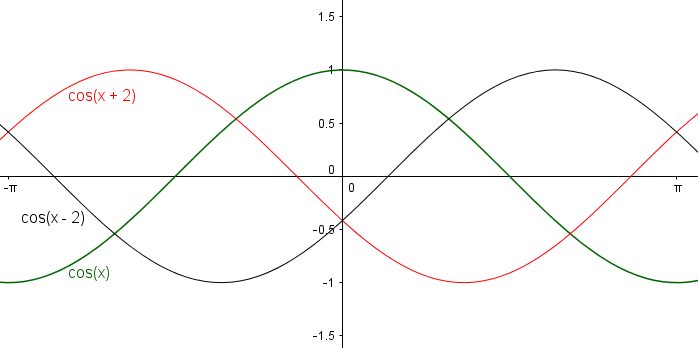
Kosinusfunktion - Verschiebung in x-Richtung
Außerdem kann die Kosinuskurve entlang der x-Achse verschoben werden.
Merke
$y = sin(x + c)$
Der Parameter $c$ verschiebt die Kosinuskurve entlang der x-Achse.
$c>0 \rightarrow$ Verschiebung nach rechts
Bei der Verschiebung entlang der x-Achse ändern sich sowohl Null- als auch Extremstellen der Funktion. Außerdem ist die Verschiebung immer nur innerhalb einer Periode ($2\cdot \pi$) sichtbar. Wird die Kosinuskurve beispielsweise um $2 \pi$ nach links verschoben, kann man diese Verschiebung nicht sehen, da die Kurve wieder deckungsgleich mit der normalen Form ist.
Teste dein neu erlerntes Wissen zur Kosinusfunktion mit unseren Übungsaufgaben! Dabei wünschen wir dir viel Spaß und Erfolg!
Weitere interessante Inhalte zum Thema
-
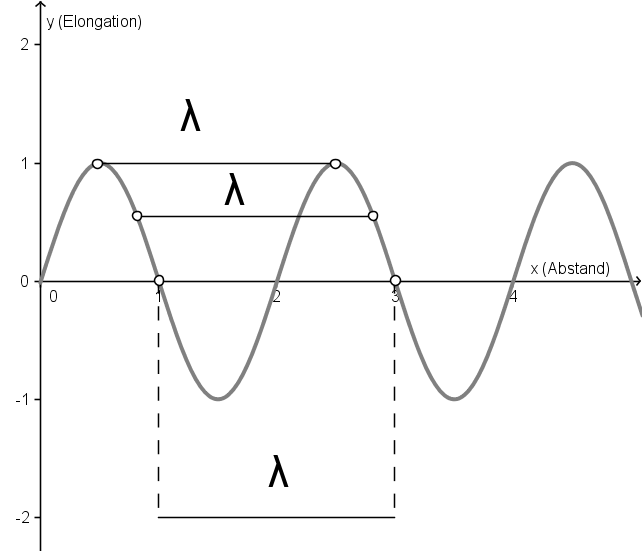
Grundbegriffe für Wellen
Vielleicht ist für Sie auch das Thema Grundbegriffe für Wellen (Schwingungen und Wellen - Grundlagen) aus unserem Online-Kurs Elektromagnetismus interessant.