Streckung, Stauchung und Periode der Sinusfunktion
In diesem Lerntext werden wir dir die verschiedenen Begrifflichkeiten und Eigenschaften der allgemeinen Sinusfunktion erklären. Dabei gehen wir auf die verschiedenen Bedeutungen der Variablen der allgemeinen Sinusfunktion genauer ein und erklären dir diese.
Was ist die allgemeine Sinusfunktion? - Definition
Die allgemeine Sinusfunktion besteht, wie der Name vermuten lässt, aus dem "Faktor" Sinus, welcher im Bezug zur Variable steht. Dieser Faktor kann jedoch durch verschiedenste Variablen verändert werden.
Sinusfunktion - Streckung, Stauchung und Periode
Nachfolgend erklären wir dir die beiden Variablen $a$ und $b$ der allgemeinen Sinusfunktion:
$y\;=\;\textcolor{orange}{a}\;\cdot \sin(\textcolor{green}{b}\;\cdot x)$
Streckungs- und Stauchungsfaktor $\textcolor{orange}{a}$
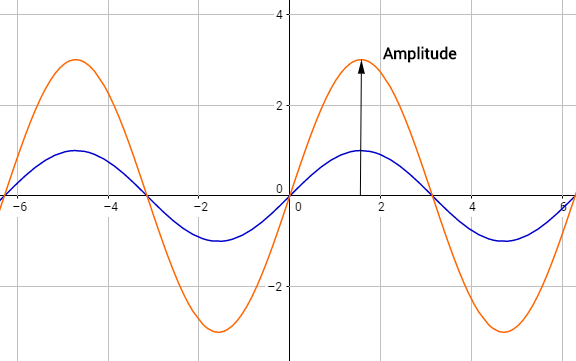
Die Variable $\textcolor{orange}{a}$ beschreibt den Streckungsfaktor der Funktion. Dieser lässt die Funktion höher verlaufen, der Ausschlag in y-Richtung wird größer. Dieser Ausschlag wird in der Mathematik Amplitude genannt. Je größer der Streckungsfaktor, desto höher verläuft die Funktion und desto größer ist die Amplitude der Funktion:
Hinweis
$\textcolor{orange}{a}$ ist zwar, wie du jetzt weißt, der Streckungsfaktor, ABER die Sinusfunktion kann auch gestaucht werden. Du kannst dir hierbei merken:
$\textcolor{orange}a>1$ (a größer 1) $\rightarrow $ Funktion ist gestreckt.
$0<\textcolor{orange}a<1$ (a liegt zwischen 0 und 1) $\rightarrow $ Funktion ist gestaucht.
Durch die Veränderung des Streckungsfaktors ändert sich auch der Wertebereich der Funktion.
Merke
Die Amplitude der Sinusfunktion wird "der größte Ausschlag nach oben und unten" genannt.
Die Variable $a$ der allgemeinen Sinusfunktion bezeichnet den Streckungsfaktor. Dieser verändert die Amplitude und damit die Wertemenge.
Periode $\textcolor{green}{b}$
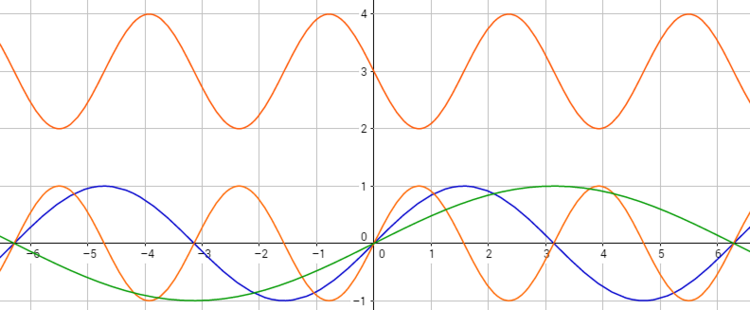
Die Sinusfunktion verläuft periodisch, das heißt, dass sich die einzelnen Abschnitte der Funktion wieder und wieder wiederholen. Die Periode der Sinusfunktion wird hierbei der sich immer wieder wiederholende Abschnitt genannt. Wenn wir den Faktor $\textcolor{green}{b}$ der Funktion verändern, ändert sich auch die Länge der Periode. Bei größerem Faktor $\textcolor{green}{b}$ wird die Periode der Funktion kürzer, bei kleinerem Faktor $\textcolor{green}{b}$ größer, bis hin zur Spiegelung der Funktion bei negativem Vorzeichen.
In der folgenden Abbildung haben wir die $\textcolor{blue}{blaue \;Sinusfunktion}$ unverändert gelassen, bei der $\textcolor{green}{grünen\; Funktion}$ den Faktor auf $0,5$ gesetzt und bei der $\textcolor{orange}{orangenen \;Funktion}$ den Faktor $2$ bzw. $-2$ gewählt. Die Funktion mit dem negativen Faktor haben wir zur besseren Übersichtlichkeit nach oben verschoben:
Merke
Die Periode beschreibt den sich wiederholenden Abschnitt der Sinusfunktion. Er kann verlängert, verkürzt oder sogar gespiegelt werden, je nachdem wie der Faktor $\textcolor{green}{b}$ der Funktion aussieht.
Die Ruhelage der Sinusfunktion
Ein weiterer Fachbegriff bei Sinusfunktionen beschreibt die Ruhelage. Diese stellt den Mittelwert zwischen Höchstpunkt und Tiefpunkt der Funktion dar. Sie wird als Gerade dargestellt. Bei keiner Verschiebung der Funktion in Richtung der y-Achse bildet die x-Achse die Ruhelage.
Zur Vertiefung dieses Themas schau auch noch einmal in die Übungen! Viel Erfolg beim Lösen der Aufgaben!
Weitere interessante Inhalte zum Thema
-
Erzwungene Schwingung- Resonanz
Vielleicht ist für Sie auch das Thema Erzwungene Schwingung- Resonanz (Elektromagnetische Schwingungen) aus unserem Online-Kurs Elektromagnetismus interessant.
-
Charakteristische Größen
Vielleicht ist für Sie auch das Thema Charakteristische Größen (Schwingungen und Wellen - Grundlagen) aus unserem Online-Kurs Elektromagnetismus interessant.