Winkelfunktion - Wie rechne ich mit dem Tangens?
Auch zu dieser Winkelfunktion findet ihr hier leicht verständliche Erklärungen.
Winkelfunktion Tangens - Definition
Der Tangens ist die dritte und letzte Winkelfunktion, die wir bearbeiten. Er beschreibt das Verhältnis zwischen einem Winkel, der Ankathete und der Gegenkathete des Winkels. Der Tangens wird mathematisch $\tan(\alpha)$ abgekürzt.
Merke
$tan(\alpha) = \frac{Gegenkathete}{Ankathete}$
Was kann man mit dem Tangens berechnen? - Formeln
Mit dem Tangens rechnest du, wenn du zwei der drei Größen, Winkel, Ankathete des Winkels und Gegenkathete des Winkels gegeben hast und die dritte Größe suchst. Das Vorgehen ist also ähnlich wie beim Sinus und Kosinus.
$tan(\alpha) = \frac{Gegenkathete}{Ankathete}$
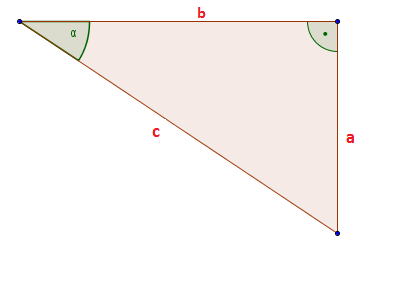
Auf das obere Bild bezogen, ergibt sich mit der Formel: $tan(\alpha) = \frac{a}{b}$
Methode
$Winkel = tan^{-1}(\frac{Gegenkathete}{Ankathete})$
$Gegenkathete = tan(Winkel)\cdot Ankathete$
$Ankathete= \frac{Gegenkathete}{tan(Winkel)}$
Auf diese Formeln kommst du durch Umformung der Grundformel $tan(\alpha) = \frac{Gegenkathete}{Ankathete}$. Daher musst du diese Formeln nicht auswendig lernen. Es ist aber dennoch hilfreich sie zu kennen. Vor allem, da du Aufgaben schneller lösen kannst, wenn du nicht erst die Formel umstellen musst.
Tangens - Beispielaufgaben mit Lösungsweg
Beispiel
Winkel
Berechnung des Winkels $\alpha$ mit dem Tangens.
$\alpha = ?, a = 5~km, b = 7~km$
$tan(\alpha) = \frac{a}{b}$
$tan(\alpha) = \frac{5~km}{7~km}$
$\alpha = tan^{-1}\frac{5}{7}$
$\alpha\approx{35,54} ^\circ$
Damit ist der Winkel ungefähr $35,5^\circ$ groß.
Gegenkathete berechnen
Beispiel
Gegenkathete
Berechnung der Länge der Gegenkathete (hier b) mit dem Tangens.
$\alpha = 60 ^\circ, a = ?, b = 7,7~mm$
$tan(\alpha) = \frac{a}{b}$
$tan(60 ^\circ) = \frac{a}{7,7~mm}$
${tan(60 ^\circ)}\cdot{7,7~mm} = a$
${a}\approx{13,34~mm}$
Die Gegenkathete ist ca. 13,34 mm lang.
Ankathete berechnen
Beispiel
Ankathete
Berechnung der Länge der Ankathete (hier c) mit dem Tangens.
$\alpha = 50 ^\circ, a = 5~m, b = ?$
$tan(\alpha) = \frac{a}{b}$
$tan(50 ^\circ) = \frac{5}{b}$
${tan(50 ^\circ)}\cdot{b} = 5~m$
$b = \frac{5~m}{tan(50 ^\circ)}$
${b} \approx {4,2~m}$
Die Ankathete ist ca. 4,2 m lang.
Jetzt hast du das nötige Wissen über das Rechnen mit dem Tangens. Überprüfe dein Wissen jetzt mit den Übungsaufgaben. Dabei wünschen wir dir viel Spaß und Erfolg!
Weitere interessante Inhalte zum Thema
-
Vektoren und Winkel
Vielleicht ist für Sie auch das Thema Vektoren und Winkel (Weitere Rechenoperationen mit Vektoren) aus unserem Online-Kurs Analytische Geometrie / Lineare Algebra (Agla) interessant.