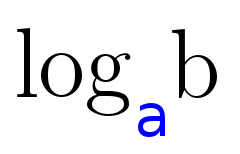Kehrwertsätze - Den Kehrwert eines Logarithmus bilden
Neben den Logarithmusgesetzen helfen dir beim Rechnen mit Logarithmen auch die sogenannten Kehrwertsätze. Zunächst sollest du dir noch einmal in Erinnerung rufen, wie die verschiedenen Bestandteile des Logarithmus heißen. Bei den Kehrwertsätzen der Logarithmen tauschen die verschiedenen Variablen nämlich ihren Platz und man kann schnell den Überblick verlieren.
Welche Bestandteile hat ein Logarithmus?
Die Variable $\textcolor{blue}{a}$ wird Basis genannt, die Variable $\textcolor{black}{b}$ Numerus oder etwas veraltet auch Logarithmand. Die Frage, die hinter dem Logarithmus steckt, lautet: Mit welcher Zahl muss ich die Basis $\textcolor{blue}{a}$ hoch nehmen, um den Numerus $\textcolor{black}{b}$ zu erhalten?
Methode
Was ist der Kehrwert?
$x~ \rightarrow \frac{1}{x}$
Kehrwert eines Logarithmus
Merke
Logarithmen können berechnet werden, indem man Basis und Numerus vertauscht und den Kehrwert bildet.
$\log_{\textcolor{blue}{a}}(\textcolor{black}{b})~=~ \frac{1}{\log_{\textcolor{black}{b}}(\textcolor{blue}{a})}$
Dieser Kehwertsatz ist ein Spezialfall des Basiswechselsatzes. Dabei wählen wir den Numerus als neue Basis.
Hinweis
Basiswechselsatz
Für den Fall, dass ein Logarithmus zur Basis $\textcolor{blue}{a}$ unbekannt ist, kann man ihn in einen Quotienten zweier Logarithmen zu einer beliebigen Basis ($\textcolor{green}{c}$) umwandeln.
$\log_{\textcolor{blue}{a}}(\textcolor{black}{b})~=~ \frac{\log_{\textcolor{green}{c}}(\textcolor{black}{b})}{\log_{\textcolor{black}{\textcolor{green}{c}}}(\textcolor{blue}{a})}$
Wir können den Basiswechselsatz also anwenden, um den ersten Kehrwertsatz zu beweisen:
$\log_{a}(b) = \frac{\log_{b}(b)}{\log_{b}(a)}$
Da $\log_{b}(b)~=~1$ erhalten wir den Satz:
$\log_{a}(b) = \frac{1}{\log_{b}(a)}$
Beispiel
$\log_{8}(2) = \frac{1}{\log_{2}(2)} = \frac{1}{3}$
Logarithmus des Kehrwerts
Merke
Ein Logarithmus des Numerus $\textcolor{black}{b}$ und der Logarithmus von dessen Kehrwert ($\frac{1}{\textcolor{black}{b}}$) unterscheiden sich nur durch das Vorzeichen:
$\log_{\textcolor{blue}{a}}(\textcolor{black}{b}) = - \log_{\textcolor{blue}{a}}(\frac{1}{\textcolor{black}{b}})$
Diese Rechenregel lässt sich mithilfe des 3. Logarithmusgesetzes herleiten. Nach dem dritten Logarithmusgesetz entspricht der Logarithmus einer Potenz dem Exponenten mal dem Logarithmus der Basis der Potenz:
$\log_{a}(b^x) = x \cdot \log_{a}(b)$
Wenden wir diese Rechenhilfe nun rückwärts auf den Logarithmus des Kehrwerts an, erhalten wir den zweiten Kehrwertsatz:
$- \log_{a}(\frac{1}{b}) = -1 \cdot \log_{a}(\frac{1}{b}) = \log_{a}((\frac{1}{b})^{-1}) = \log_{a}(b)$
Beispiel
$\log_{2}(0,25) = - \log_{2}(\frac{1}{0,25}) = - \log_{2}(40) = - 2$
Doppel-Kehrwertsatz
Merke
Ein Logarithmus einer Zahl ist gleich dem Logarithmus, bei dem sowohl von der Basis als auch vom Numerus der Kehrwert gebildet wurde:
$\log_{\textcolor{blue}{a}}(\textcolor{black}{b}) = \log_{\frac{1}{\textcolor{blue}{a}}}(\frac{1}{\textcolor{black}{b}})$
Beispiel
$\log_{0,25}(\frac{1}{16})~=~\log_{\frac{1}{0,25}}(1~:~ \frac{1}{16})~=~\log_{4}(16) = 2$
Kehrwertsätze des Logarithmus - Übersicht
Hier findest du eine Übersicht über alle Kehrwertsätze des Logarithmus:
Merke
- Kehrwert eines Logarithmus $\log_{\textcolor{blue}{a}}(\textcolor{black}{b})~=~ \frac{1}{\log_{\textcolor{black}{b}}(\textcolor{blue}{a})}$
- Logarithmus eines Kehrwerts $\log_{\textcolor{blue}{a}}(\textcolor{black}{b}) = - \log_{\textcolor{blue}{a}}(\frac{1}{\textcolor{black}{b}})$
- Doppel-Kehrwertsatz $\log_{\textcolor{blue}{a}}(\textcolor{black}{b}) = \log_{\frac{1}{\textcolor{blue}{a}}}(\frac{1}{\textcolor{black}{b}})$
Teste nun dein neu erlerntes Wissen mit unseren Übungsaufgaben!
Weitere interessante Inhalte zum Thema
-
Logarithmusfunktionen
Vielleicht ist für Sie auch das Thema Logarithmusfunktionen (Funktionsklassen) aus unserem Online-Kurs Weiterführende Aufgaben der Analysis (Analysis 2) interessant.
-
Normierung eines Vektors
Vielleicht ist für Sie auch das Thema Normierung eines Vektors (Weitere Rechenoperationen mit Vektoren) aus unserem Online-Kurs Analytische Geometrie / Lineare Algebra (Agla) interessant.