Polynomdivision mit Rest- Bedeutung und Erklärung
Die Polynomdivision ist eine Methode zur Berechnung von Nullstellen von Funktionen. Sie dient dazu Terme zu vereinfachen. In diesem Kapitel werden wir uns anschauen was passiert, wenn wir die Polynomdivision durchführen, aber ein Rest bei der Division übrig bleibt.
Polynomdivision - Wiederholung
Methode
Die Grundlage für dieses Kapitel bildet das Wissen über die Polynomdivision und Polynomdivision - Nullstellen berechnen. Die Themenseiten dazu kannst du durch klicken auf die jeweiligen Begriffe erreichen.
Die Polynomdivision wird verwendet, um Nullstellen von Funktionen zu berechnen, bei denen wir die pq-Formel nicht verwenden können. Mit ihr vereinfachen wir die Funktionen soweit, bis wir die pq-Formel anwenden können.
Doch wenn wir die Nullstellen einer Funktion berechnen wollen und keine Nullstelle gegeben haben, dann wird es schwer die Polynomdivision durchzuführen. In diesem Fall müssen wir eine Nullstelle erraten. Hierfür schauen wir uns die Teiler des absoluten Gliedes an und probieren diese nacheinander aus. In manchen Fällen kann es jedoch sein, dass die Polynomdivision nicht ohne Rest aufgeht. Das sieht dann wie folgt aus:
Polynomdivision - Beispielaufgabe
Beispiel
Führe die Polynomdivision zu folgender Funktion durch: $9x^3 + 15x^2 + 12x + 6$.
Die Koeffizienten sind ganzzahlig, daher können wir uns die Teiler des absoluten Gliedes betrachten. Diese sind die sechs Zahlen $\pm1, \pm2$ und $\pm3$. Testen wir in der Polynomdivision, für den Fall, dass an Punkt $P_{-3}(-3|x)$ eine Nullstelle ist. Die Polynomdivision sieht dann wie folgt aus:
$(9x^3 + 15x^2 + 12x + 6):(x+3)=$
$-(\;9x^3+27x^2)$
—————————————————
$\;\;\;\;\;\;\;\;-12x^2+12x$
$-(\;\;\;\;\;\;\;\;-12x^2-36x)$
—————————————————
$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;48x+6$
$-(\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;48x+144)$
—————————————————
$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\underline{-138}$
Erklärung der Beispielaufgabe
Anhand des Beispiels sehen wir, dass eine Polynomdivision nicht immer aufgeht. Die Lösung der Polynomdivision hat einen Rest ergeben, sodass klar ist, dass an der Stelle $P_{-3}(-3|x)$ keine Nullstelle vorhanden ist. Die Lösung der Polynomdivision wird wie folgt aufgeschrieben:
$9x^2 - 12x + 48\;$ Rest $-138$
Da es bei einer Division jedoch keinen Rest gibt, schreiben wir auch auf, durch welchen Wert wir die $-138$ nicht teilen konnten. Somit ergibt sich:
$\large{9x^2 - 12x + 48-\frac{138}{x+3}}$
Merke
Bei einer Polynomdivision kann eine Lösung mit Rest entstehen. Das bedeutet, dass an dieser Stelle keine Nullstelle der Funktion ist.
Wir schreiben den Rest als Addition oder Subtraktion als Bruch $\large{\frac{Rest}{Divisor}}$ auf.
Zur Vertiefung dieses Themas schau auch noch einmal in die Übungen! Dabei wünschen wir dir viel Spaß und Erfolg!
Weitere interessante Inhalte zum Thema
-
Gleichungen durch Polynomdivision lösen
Vielleicht ist für Sie auch das Thema Gleichungen durch Polynomdivision lösen (Gleichungen lösen) aus unserem Online-Kurs Vorkenntnisse zur Analysis interessant.
-
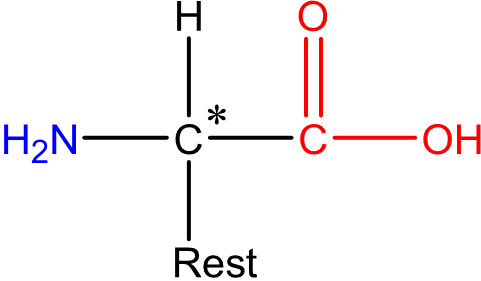
Aminosäuren = Grundbaustein der Proteine
Vielleicht ist für Sie auch das Thema Aminosäuren = Grundbaustein der Proteine (Naturstoffchemie) aus unserem Online-Kurs Organische Chemie interessant.