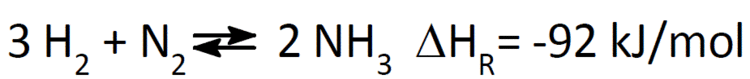Quadratwurzeln mittels Heron-Verfahren bestimmen

Mit dem Heronverfahren kannst du die Quadratwurzel einer Zahl näherungsweise bestimmen ohne einen Taschenrechner zu benutzen. Dies bezieht sich natürlich nur auf Quadratwurzeln, die keine ganze Zahl ergeben.

Bei welchen Quadratwurzeln kann man das Heronverfahren anwenden?

$\textcolor{red}{HERONVERFAHREN~NICHT~ANWENDEN}$: $\sqrt[]{4} = 2~$, $\sqrt[]{16} = 4~$, $\sqrt[]{25} = 5~$...

$\textcolor{green}{HERONVERFAHREN~ANWENDEN}$: $\sqrt[]{2} \approx 1,41~$,$\sqrt[]{12} \approx 3,46~$,$\sqrt[]{30} \approx 5,48~$...

Du solltest zunächst lernen, wie du das Heronverfahren anwendest. Der mathematische Hintergrund ist sehr komplex, weshalb es ratsam ist, das Vorgehen möglichst exakt einzuüben.

Das Heronverfahren - Schritt für Schritt anwenden

Beispielaufgabe:  $\sqrt[]{2} =$?

1. Schritt: Ergebnisbereich abschätzen

Bevor wir das Heronverfahren anwenden können, müssen wir zunächst abschätzen in welchem Bereich die gesuchte Quadratwurzel liegen wird. Dazu nimmt man die nächst kleinere bzw. größere Quadratwurzel, die eine glatte Zahl ergibt. In unserem Beispiel bedeutet das:

$\sqrt[]{1} < \sqrt[]{2} < \sqrt[]{4}$

Daraus ergibt sich: $1 < \sqrt[]{2} < 2$

Unser Ergebnisbereich $[\textcolor{blue}{a}; \textcolor{red}{b}]$ ist also $[\textcolor{blue}{1}; \textcolor{red}{2}]$.

Die Wurzel aus zwei liegt also irgendwo zwischen $1$ und $2$. Wo genau können wir noch nicht sagen. Um diesen Wert genauer zu bestimmen, nutzen wir das Heronverfahren.

2. Schritt: Tabelle aufstellen

Das Heronverfahren besteht aus einer Tabelle, die wie folgt aussieht:

$\textcolor{black}{a~~~~~~~~~\frac{b}{a}~~~~~...\sqrt[]{2}...~~~~~\frac{a + b}{2}}$

Setzen wir für die Werte $a$ und $b$ nun unseren Ergebnisbereich von $1$ und $2$ ein, erhalten wir die erste Zeile der Tabelle:

$\textcolor{black}{a~~~~~~~~~~~~~~~~~~~~~\frac{b}{a}~~~~~~~~...\sqrt[]{2}...~~~~~~~~\frac{a + b}{2}}$

$\textcolor{green}{a_0 = 1~~~~~~~~~~~~\frac{2}{1}~~~~~~~1}$

Die erste Zeile gibt uns zunächst nur die Informationen, die wir schon hatten. In der dritten Spalte tragen wir den Ergebnisbereiche ein, der sich aus den ersten beiden Spalten ergibt. In der vierten Spalte berechnen wir den Mittelwert der beiden Werte $a$ und $b$. Dieser Wert ist deshalb wichtig, da man ihn in der nächsten Zeile als den "neuen" $a$ wert einsetzt.

$\textcolor{black}{a~~~~~~~~~~~~~~~~~~~~~\frac{b}{a}~~~~~~~~~~~~~~~~~~~~~~~...\sqrt[]{2}...~~~~~~~~~~~~~~~~~\frac{a + b}{2}}$

$\textcolor{green}{a_0 = 1~~~~~~~~~~~~\frac{2}{1}=2~~~~~~~~~~~~~~1}$

$\textcolor{blue}{a_1 = 1,5~~~~~~~\frac{2}{1,5}=1,\overline{3} ~~~~~~~1,\overline{3}}$

Wir erhalten in jeder Zeile zwei neue Werte $a$ und $b$, die den Bereich für $\sqrt[]{2}$ verkleinern. Dabei muss $a$ nicht immer der kleinere Wert sein. Je nachdem ob $a$ oder $b$ der kleinere Wert ist, schreiben wir in der dritten Spalte entweder $a

$\textcolor{black}{a~~~~~~~~~~~~~~~~~~~~~~~~~~~\frac{b}{a}~~~~~~~~~~~~~~~~~~~~~~~~~~~~~...\sqrt[]{2}...~~~~~~~~~~~~~~~~~~~~~~~\frac{a + b}{2}}$

$\textcolor{green}{a_0 = 1~~~~~~~~~~~~~~~~~~\frac{2}{1}=2~~~~~~~~~~~~~~~~~~~~~~1}$

$\textcolor{blue}{a_1 = 1,5~~~~~~~~~~~~~\frac{2}{1,5}=1,\overline{3} ~~~~~~~~~~~~~~~1,\overline{3}}$

$\textcolor{orange}{a_2 = 1,416~~~~~~~\frac{2}{1,416}=1,411 ~~~~~~~1,411}$

Theoretisch könnten wir dieses Verfahren noch unendlich oft wiederholen. Allerdings ändern sich die beiden Näherungswerte $a$ und $b$ kaum noch.

3. Schritt: Näherungswert angeben

In unserem Beispiel können wir nach der dritten Zeile eine ungefähre Näherung von $\sqrt[]{2} \approx 1,41$ angeben. Dies stimmt auch mit dem Ergebnis des Taschenrechners überein.

Es gibt mehrere Varianten des Heronverfahrens. Diejenige, die wir hier besprochen haben, ist die einfachste, führt aber genauso zum Ziel.

Teste dein neu erlerntes Wissen zum Heronverfahren in unseren Übungsaufgaben! Wir wünschen dir dabei viel Erfolg und Spaß!