Grundrechenarten - Multiplizieren einfach erklärt
Die Multiplikation ist eine der Grundrechenarten in der Mathematik. Diese wirst du im Laufe deiner Schulzeit noch sehr häufig finden, solltest sie also beherrschen. Dazu helfen wir dir nicht nur mit den Erklärungen in diesem Text und verschiedenen Beispielen, sondern auch mit Übungen.
Welche Eigenschaften hat die Multiplikation?
Das Multiplizieren ist in der Mathematik eine vereinfachte Form der Addition. Wenn du eine Zahl sehr häufig mit sich selbst addieren musst, dann ist die einfachere Schreibweise die Multiplikation. Mit ihr kannst du also schneller große Zahlenmengen zusammenrechnen.
Natürlich haben die verschiedenen Terme in so einer Rechnung auch spezielle Namen.
Merke
- Bei der Multiplikation heißen die Terme, die multipliziert werden, Faktoren.
- Das Zeichen nennt sich Mal-Zeichen und wird so geschrieben: $\large {\cdot}$
- Die Multiplikation ist eine Kurzform der Addition.
Multiplizieren - Beispielaufgaben
Schauen wir uns das Ganze einmal praktisch an.
Wenn wir rechnen wollen:
$ 5 \; + \; 5 \; + \; 5 \; + \; 5 \; + \; 5 \; + \; 5 \; + \; 5 \; $ erhalten wir $35$.
Wir addieren also $7$ Mal die $5$ miteinander. Genau das ist schon der Ansatz für die Multiplikation.
$ 7 \; \cdot \; 5 \; = \; 35$
Wir sehen also, dass die Multiplikation eine Kurzform der Addition ist. Du könntest die $5$ auch ausschreiben und mit sich selbst addieren um so die Lösung erhalten.
Schauen wir uns einmal weitere Beispiele an:
$ 3 \; \cdot \; 4 \; = \; 12$
$ 6 \; \cdot \; 5 \; = \; 30$
$ 2 \; \cdot \; 12 \; = \; 24$
$ 9 \; \cdot \; 8 \; = \; 72$
$ 1 \; \cdot \; 3 \; = \; 3$
Wie funktioniert das schriftliche Multiplizieren?
Wenn du große Zahlen hast und diese miteinander Multiplizieren musst, kannst du die schriftliche Multiplikation verwenden. Diese haben wir in der folgenden Abbildung benutzt.
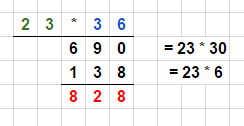
Bei der schriftlichen Multiplikation musst du also die Zahlen, die du miteinander multiplizieren willst, nebeneinander schreiben. Dann rechnest du einzeln die Zahlen miteinander mal. Im Folgenden ein Beispiel:
$\textcolor{green}{23} \cdot \textcolor{blue}{36}$
Du gehst also Schritt für Schritt vor und rechnest zuerst die $\textcolor{blue}{30}$ mal die $\textcolor{green}{3}$. Du erhälst $\textcolor{brown}{90}$. Hinzu kommen aus Schritt zwei:
$\textcolor{green}{20} \cdot \textcolor{blue}{30}$. Das Ergebnis ist $\textcolor{brown}{600}$. Diese beiden Werte addierst du und es ergibt sich $\textcolor{brown}{690}$.
Schritt drei ist $\textcolor{blue}{6} \cdot \textcolor{green}{3}$. Das Ergebnis ist $\textcolor{brown}{18}$.
Der nächste Schritt ist die Multiplikation von $\textcolor{blue}{6}$ mit $\textcolor{green}{20}$. Es ergibt sich $\textcolor{brown}{120}$. Jetzt addierst du die beiden Ergebnisse $\textcolor{brown}{18}$ und $\textcolor{brown}{120}$ und erhälst $\textcolor{brown}{138}$.
Der letzte Schritt ist die Addition der beiden Werte, also $\textcolor{brown}{690} + \textcolor{brown}{138}$. Wir erhalten $\textcolor{brown}{828}$. Diese Zahl schreiben wir unter einen Strich, damit wir sehen, was die Rechnung und was die Lösung ist.
Genauso gehst du auch bei den weiteren Beispielen vor.
Zur Vertiefung der Vorgehensweise beim Mulitiplizieren schau auch noch einmal in die Übungen! Dabei wünschen wir dir viel Spaß und Erfolg!
Weitere interessante Inhalte zum Thema
-
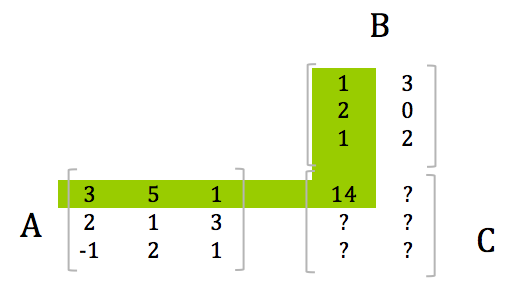
Multiplikation von Matrizen
Vielleicht ist für Sie auch das Thema Multiplikation von Matrizen (Rechenregeln für Matrizen) aus unserem Online-Kurs Analytische Geometrie / Lineare Algebra (Agla) interessant.
-
Lewis-Schreibweise
Vielleicht ist für Sie auch das Thema Lewis-Schreibweise (Bindungsarten) aus unserem Online-Kurs Anorganische Chemie interessant.