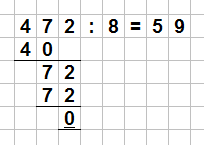Teilbarkeitsregeln - Endziffernregel einfach erklärt
Die Endziffernregel ist eine der Teilbarkeitsregeln in der Mathematik. Mit ihr lässt sich schnell erkennen, durch welche Zahlen eine ausgewählte Zahl teilbar ist. In diesem Kapitel befassen wir uns mit der Teilbarkeit durch die Zahlen $2,4,5,8$ und $10$ mithilfe der Endziffernregel.
Endziffernregeln - Übersicht
Merke
Eine Zahl ist durch $2$ teilbar, wenn ihre letzte Ziffer gerade ist.
Eine Zahl ist durch $4$ teilbar, wenn die Zahl, die mit den letzten beiden Ziffern gebildet wird, durch $4$ teilbar ist.
Eine Zahl ist durch $5$ teilbar, wenn die letzte Ziffer eine $0$ oder eine $5$ ist.
Eine Zahl ist durch $8$ teilbar, wenn die Zahl, die mit den letzten drei Ziffern gebildet wird, durch $8$ teilbar ist.
Eine Zahl ist durch $10$ teilbar, wenn die Endziffer eine $0$ ist.
Dieses Wissen vertiefen wir anhand von Beispielen zu jeder Zahl.
Endziffernregel zur Zahl 2
Um zu prüfen, ob eine Zahl durch $2$ teilbar ist, ohne einen Rest bei der Division zu hinterlassen, zählt die letzte Ziffer. Wenn diese Ziffer gerade ist, also $2, 4, 6, 8$ oder $0$, dann ist die Zahl durch $2$ teilbar. Hierzu ein Beispiel:
Beispiel
Prüfe, ob die Zahl $3058$ durch $2$ teilbar ist.
Laut der Regel ist die Zahl $3058$ durch $2$ teilbar, weil die letzte Ziffer gerade ist. Durch eine Probe erkennen wir:
$3058 \; : \; 2 \; = \; 1529$
Somit ist die Zahl durch $2$ teilbar.
Endziffernregel zur Zahl 4
Damit eine Zahl durch $4$ teilbar ist, muss die Zahl, die aus den letzten beiden Ziffern besteht, durch $4$ teilbar sein. Im Beispiel sehen wir das genauer:
Beispiel
Ist die Zahl $3056$ durch $4$ teilbar?
Die Lösung lautet: Ja, denn:
$56 \;:\;4\;=\;14$ Die letzten beiden Ziffern bilden die Zahl $56$ und die Zahl $56$ ist durch $4$ teilbar. Die Lösung für die gesamte Division lautet:
$3056\;:4\;=\;764$
Endziffernregel zur Zahl 5
Eine Zahl ist genau dann durch $5$ teilbar, wenn die letzte Ziffer eine $0$ oder eine $5$ ist. Dazu zwei Beispiele:
Beispiel
Lässt sich die Zahl $125$ durch $5$ teilen?
Ja, die Zahl $125$ lässt sich durch $5$ teilen, weil die letzte Ziffer eine $5$ ist.
Lässt sich die Zahl $36$ durch $5$ teilen?
Nein, die Zahl $36$ lässt sich nicht durch $5$ teilen, da die letzte Ziffer weder eine $0$ noch eine $5$ ist.
Endziffernregel zur Zahl 8
Die Zahl $8$ und ihre Teilbarkeitsregel ist etwas schwieriger. Denn um zu Prüfen, ob eine Zahl durch $8$ teilbar ist, muss die Zahl, die aus den letzten drei Ziffern gebildet wird, durch $8$ teilbar sein. Diese Regel ist nur bei sehr großen Zahlen hilfreich.
Beispiel
Ist die Zahl $86472$ durch $8$ teilbar?
Laut der Regel schauen wir uns nur die letzten drei Ziffern an und dividieren diese Zahl durch $8$. In einer schriftlichen Division sieht das dann so aus:
Da die Zahl $472$ durch $8$ teilbar ist, ist somit auch die gesamte Zahl durch $8$ teilbar. Die Zahl $86472$ ist also durch $8$ teilbar.
Endziffernregel zur Zahl 10
Eine Zahl ist durch $10$ teilbar, wenn die letzte Ziffer eine $0$ ist. In unserem Beispiel sehen wir dies genauer:
Beispiel
Kann man die Zahl $1592$ durch $10$ teilen?
Nein, die letzte Ziffer der Zahl $1592$ ist keine $0$ und somit ist die Zahl $1592$ nicht durch $10$ teilbar.
Kann man die Zahl $1590$ durch $10$ teilen?
Ja, denn die letzte Ziffer der Zahl $1590$ ist eine $0$ und somit kann die Zahl $1590$ durch $10$ geteilt werden. Die Lösung ist $159$.
Zur Vertiefung dieses Themas schau auch noch einmal in die Übungen!
Weitere interessante Inhalte zum Thema
-
Lineare Gleichungen lösen
Vielleicht ist für Sie auch das Thema Lineare Gleichungen lösen (Gleichungen lösen) aus unserem Online-Kurs Vorkenntnisse zur Analysis interessant.
-
Entwicklung der Quantentheorie
Vielleicht ist für Sie auch das Thema Entwicklung der Quantentheorie aus unserem Online-Kurs Quanteneffekte & Struktur der Materie interessant.