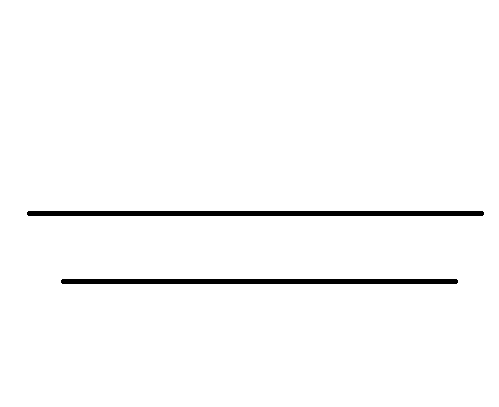Mathematik 6. Klasse - Wichtige Themen in der Übersicht
Im Mathematikunterricht der 6. Klasse lernst du eine sehr wichtige neue Gruppe von Zahlen kennen: Die rationalen Zahlen. Die rationalen Zahlen werden auch Bruchzahlen genannt und besitzen eigene Rechenregeln für Addition, Subtraktion, Multiplikation und Division. Gleichzeitig gibt die Bruchrechnung einen ersten Einblick in den Umgang mit Prozentangaben. Neben Brüchen beschäftigt ihr euch vor allem mit weiteren Themen der Geometrie. Nachdem ihr in der 5. Klasse die Grundlagen dieser mathematischen Disziplin erlernt habt, erfahrt ihr in der 6. Klasse alles über Winkel. Ihr lernt die verschiedenen Arten von Winkeln kennen, lernt die Größe von Winkeln zu messen und Winkel zu zeichnen. Darüber hinaus lernt ihr, wie man die Winkel an Geradenkreuzungen nennt. Neben den Winkeln lernt ihr auch erste geometrische Grundkonstruktionen kennen, wie zum Beispiel das Einzeichnen einer Winkelhalbierenden oder die Spiegelung einer Figur an einer Achse oder an einem Punkt.
Auf dieser Seite findest du nun eine kurze Zusammenfassung der wichtigsten Themen des Mathematikunterrichts der 6. Klasse. Wichtige Begriffe werden hier auch nochmals erklärt.
Begriffe zur Zahlenlehre und Rechengesetzen
Bruchzahl
Ein Bruch steht für eine Division. Sowohl die Zahl im Zähler als auch die Zahl im Nenner muss eine ganze Zahl sein. Die Zahl im Zähler kann kleiner oder größer als die Zahl im Nenner sein. Wenn der Zähler größer als der Nenner ist, bezeichnet man den Bruch als unechten Bruch.
$\large{\frac{\textcolor{red}{a}}{\textcolor{blue}{b}} = \frac{\textcolor{red}{Zähler}}{\textcolor{blue}{Nenner}}}$
Merksatz: $\textcolor{red}{Zäh}\textcolor{blue}{ne}$
Brüche addieren
Brüche mit gleichem Nenner werden addiert, indem die Zähler addiert werden und der Nenner beibehalten wird.
Brüche mit unterschiedlichen Nennern müssen zunächst gleichnamig gemacht werden. ("Gleichnamig machen" bedeutet, die Brüche so zu erweitern bzw. zu kürzen bis beide Brüche den gleichen Nenner besitzen.)
Beispiel
$\large{\frac{\textcolor{red}{a}}{\textcolor{blue}{b}} = \frac{\textcolor{red}{2}}{\textcolor{blue}{4}}}+ \frac{\textcolor{red}{1}}{\textcolor{blue}{4}} = \large{\frac{\textcolor{red}{(2+1)}}{\textcolor{blue}{4}}} = \large{\frac{\textcolor{red}{3}}{\textcolor{blue}{4}}}$
Brüche subtrahieren
Brüche mit gleichem Nenner werden subtrahiert, indem die Zähler subtrahiert werden und der Nenner beibehalten wird.
Brüche mit unterschiedlichen Nennern müssen zunächst gleichnamig gemacht werden. ("Gleichnamig machen" bedeutet, die Brüche so zu erweitern bzw. zu kürzen bis beide Brüche den gleichen Nenner besitzen.)
Beispiel
$\large{\frac{\textcolor{red}{4}}{\textcolor{blue}{6}}}- \frac{\textcolor{red}{3}}{\textcolor{blue}{6}} = \large{\frac{\textcolor{red}{(4-3)}}{\textcolor{blue}{6}}} = \large{\frac{\textcolor{red}{1}}{\textcolor{blue}{6}}}$
Brüche multiplizieren
Brüche werden miteinander multipliziert, indem Zähler mit Zähler und Nenner mit Nenner multipliziert wird. Als Ergebnis erhält man wieder einen Bruch.
$\large{\frac{\textcolor{green}{a}}{\textcolor{red}{b}} \cdot \frac{\textcolor{green}{c}}{\textcolor{red}{d}} = \frac{\textcolor{green}{a} \cdot \textcolor{green}{c}}{\textcolor{red}{b} \cdot \textcolor{red}{d}}}$
Beispiel
$\large{\frac{\textcolor{green}{4}}{\textcolor{red}{5}} \cdot \frac{\textcolor{green}{3}}{\textcolor{red}{7}} = \frac{\textcolor{green}{4} \cdot \textcolor{green}{3}}{\textcolor{red}{5} \cdot \textcolor{red}{7}} = \frac{\textcolor{green}{12}}{\textcolor{red}{35}}}$
Brüche dividieren
Brüche werden dividiert, indem man den ersten Bruch mit dem Kehrwert des zweiten Bruchs multipliziert. Den Kehrwert bildest du, indem du Zähler und Nenner des Bruchs vertauscht.
$\Large{\frac{a}{b} : \frac{\textcolor{red}{c}}{\textcolor{green}{d}} = \frac{a}{b} \cdot \frac{\textcolor{green}{d}}{\textcolor{red}{c}} = \frac{a~ \cdot \textcolor{green}{d}}{b~ \cdot \textcolor{red}{c}}}$
Beispiel
$\large{\frac{\textcolor{green}{4}}{\textcolor{red}{5}} : \frac{\textcolor{green}{3}}{\textcolor{red}{7}} = \frac{\textcolor{green}{4}}{\textcolor{red}{5}} \cdot \frac{\textcolor{green}{7}}{\textcolor{red}{3}} = \frac{\textcolor{green}{4} \cdot \textcolor{green}{7}}{\textcolor{red}{5} \cdot \textcolor{red}{3}} = \frac{\textcolor{green}{28}}{\textcolor{red}{15}}}$
Brüche erweitern
Brüche werden erweitert, indem Zähler und Nenner mit derselben Zahl multipliziert werden.
Brüche kürzen
Merke
Brüche werden gekürzt, indem Zähler und Nenner durch dieselbe Zahl dividiert werden.
Brüche und Prozentsätze umrechnen
Merke
Um einen Prozentsatz in einen Bruch umzuformen, schreibst du die Prozentangabe ohne Prozentzeichen in den Zähler und eine $100$ in den Nenner. Meistens kannst du diesen Bruch dann noch kürzen.
$ 40~\%~=~\frac{40}{100}~=~\frac{2}{5}$
Um einen Bruch in einen Prozentsatz umzuwandeln, musst du den Bruch zunächst so erweitern oder kürzen, dass im Nenner die Zahl $100$ steht. Der Zähler entspricht dann dem Prozentsatz.
$\frac{3}{5}~=~\frac{60}{100}~=~60~\%~$
Brucharten
Merke
Bei echten Brüchen hat der Zähler einen kleineren Wert als der Nenner. Besitzt der Zähler den Wert $1$, bezeichnet man den Bruch als Stammbruch.
Bei unechten Brüchen hat der Zähler den gleichen oder einen größeren Wert als der Nenner. Unechte Brüche, bei denen der Zähler ein Vielfaches des Nenners ist, nennt man auch Scheinbrüche, da sie sich durch Kürzen in ganze Zahlen umwandeln lassen.
Gemischte Zahlen bestehen aus einer ganzen Zahl und einem Bruch. Jeder unechte Bruch lässt sich entweder in eine ganze Zahl oder eine gemischte Zahl umwandeln.
Dezimalbrüche besitzen eine Zehnerpotenz im Nenner ($10, 100, 1000...$) und lassen sich als Dezimalzahlen schreiben.
Begriffe der Geometrie
Winkel
Merke
Ein Winkel beschreibt die Größe der Neigung zwischen zwei Strahlen bzw. Strecken. Die Einheit, in der wir die Größe eines Winkels angeben, ist Grad (°). Bezeichnet werden die Winkel für gewöhnlich mit griechischen Buchstaben, wie α = Alpha oder β = Beta.
Winkelarten
Um einen Überblick über alle Winkelarten zu bekommen, kann man die Winkelarten in 3 Gruppen einteilen:
Die 1. Gruppe beinhaltet jene Winkelarten, dessen Winkel durch zwei Halbgeraden, die von dem gleichen Punkt aus starten, gebildet werden.
Die 2. und 3. Gruppe werden von den sogenannten "Winkelpaaren" gebildet. Winkelpaare sind zwei Winkel an sich schneidenen Geraden.
Schaue dir zu den Winkelarten nochmal hier drunter die Abbildungen zu den jeweiligen Gruppen an!
Merke
Zur 1. Gruppe gehören:
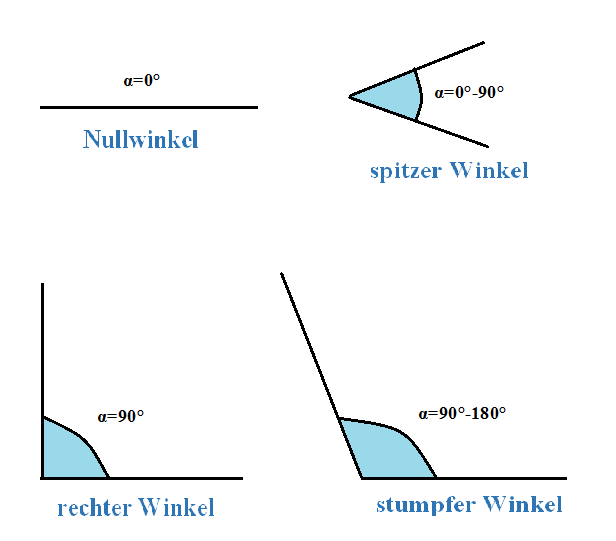
- der Nullwinkel
- der spitze Winkel
- der rechte Winkel
- der stumpfe Winkel
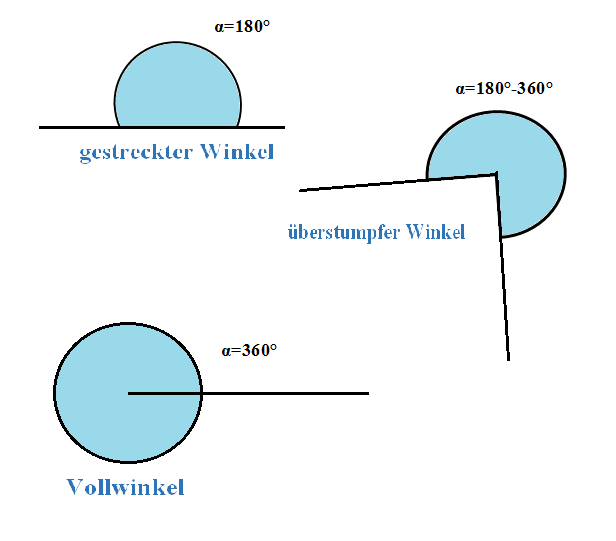
- der gestreckte Winkel
- der überstumpfe Winkel
- der Vollwinkel
Nullwinkel: Der Nullwinkel beträgt immer 0°. Die beiden Schenkel, die den Winkel bilden, liegen also aufeinander.
Spitzer Winkel: Die Winkel dieser Winkelart sind größer als 0° und kleiner als 90°.
Rechter Winkel: Der rechte Winkel ist immer exakt 90° groß.
Stumpfer Winkel: Die Winkel dieser Winkelart sind größer als 90° und kleiner als 180°.
Gestreckter Winkel: Der gestreckte Winkel beträgt immer exakt 180°. Die beiden Schenkel, die den Winkel bilden, bilden zusammen eine Gerade.
Überstumpfer Winkel: Ist ein Winkel größer als 180° und kleiner als 360°, gehört er zu den überstumpfen Winkeln.
Vollwinkel: Ein Winkel ist dann ein Vollwinkel, wenn er exakt 360° groß ist. Auch hier liegen beide Schenkel aufeinander.
Merksatz: "Wenn der Mond voll ist, haben wir Vollmond und er sieht aus wie ein runder Kreis, wie der Vollwinkel."
Merke
Zur 2. Gruppe gehören die Scheitelwinkel und die Stufenwinkel.
Scheitelwinkel: Wenn sich zwei Geraden schneiden, bezeichnet man die zwei Winkel, die sich gegenüberliegen, als Scheitelwinkel (hier: α und β). Zwei Scheitelwinkel sind immer gleich groß.
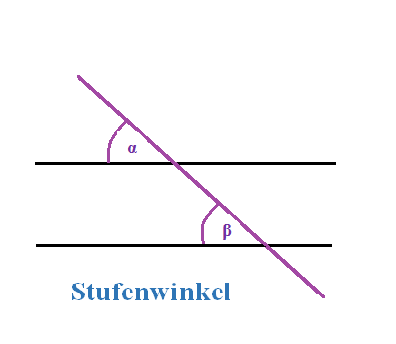
Stufenwinkel: Zwei Stufenwinkel entstehen, wenn zwei Parallelen von einer Geraden geschnitten werden. Stufenwinkel (hier α und β) sind immer gleich groß.
Merke
Zur 3. Gruppe gehören die Nebenwinkel.
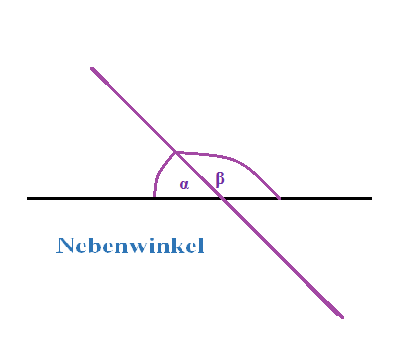
Nebenwinkel: Wenn sich zwei Geraden schneiden, bezeichnet man die Winkel, die nebeneinander liegen, als Nebenwinkel. Die Summe von zwei Nebenwinkeln beträgt immer $180^\circ$.
Winkelhalbierende
Merke
Eine Winkelhalbierende ist eine (Halb-) Gerade, die einen Winkel in zwei gleich große Hälften teilt.
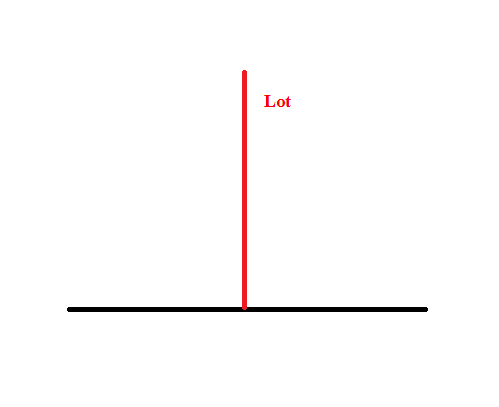
Lot
Merke
Als Lot bezeichnet man eine Gerade, die senkrecht auf einer anderen Geraden steht.
Parallelen
Merke
Als parallel bezeichnet man zwei Geraden (oder Strecken oder Halbgeraden), deren Abstand zueinander an jeder Stelle gleich groß ist. Solche Geraden (bzw. Strecken oder Halbgeraden) werden auch als Parallelen bezeichnet. Zwei Parallelen schneiden sich nicht.
Punktspiegelung
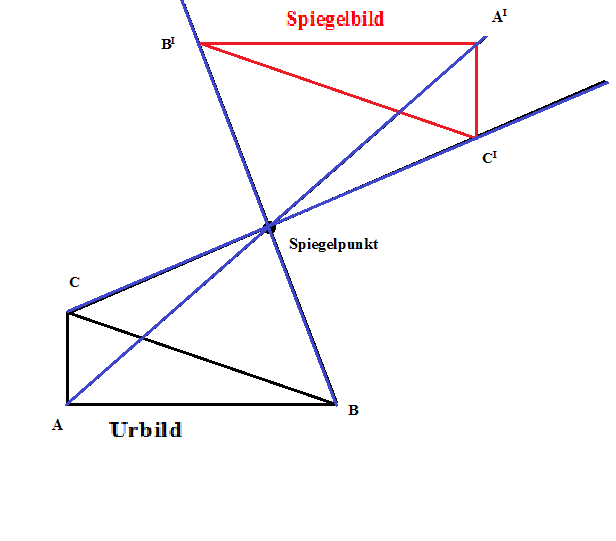
Merke
Bei der Punktspiegelung wird eine Figur an einem Spiegelpunkt gespiegelt. Dies ist identisch mit einer Drehung um den Spiegelpunkt um $180^\circ$. Die Originalfigur, also das Urbild, und das Spiegelbild sind deckungsgleich.
Achsenspiegelung
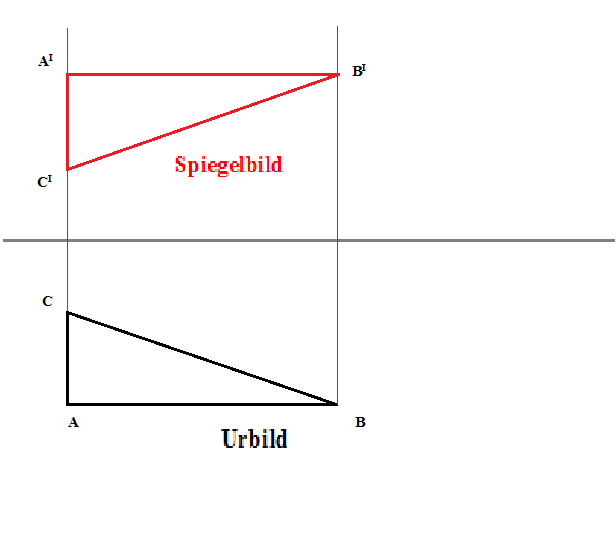
Merke
Bei der Achsenspiegelung wird eine Figur an einer Achsengeraden gespiegelt. Die Originalfigur, also das Urbild, und das Spiegelbild sind deckungsgleich.
Jetzt weißt du, welche Begriffe und Themen dich in der 6. Klasse erwarten. Teste dein Wissen jetzt in den Übungen. Viel Erfolg beim Lernen!
Weitere interessante Inhalte zum Thema
-
Klassen
Vielleicht ist für Sie auch das Thema Klassen (Beschreibende Statistik) aus unserem Online-Kurs Stochastik interessant.
-
Logarithmusfunktionen
Vielleicht ist für Sie auch das Thema Logarithmusfunktionen (Funktionsklassen) aus unserem Online-Kurs Weiterführende Aufgaben der Analysis (Analysis 2) interessant.