Mit Baumdiagrammen Wahrscheinlichkeiten berechnen

Beim Rechnen mit Wahrscheinlichkeiten kann man schnell den Überblick verlieren. Mithilfe eines Baumdiagramms kannst du die Wahrscheinlichkeiten von Wahrscheinlichkeitsversuchen ordnen und somit einfacher berechnen. Ein Baumdiagramm gibt die verschiedenen Wahrscheinlichkeiten bzw. Ausgänge eines Wahrscheinlichkeitsexperiments an. Der große Vorteil solcher Baumdiagramme ist, dass du auch mehrstufige Experimente übersichtlich darstellen kannst.

Wie sehen einfache Baumdiagramme aus?

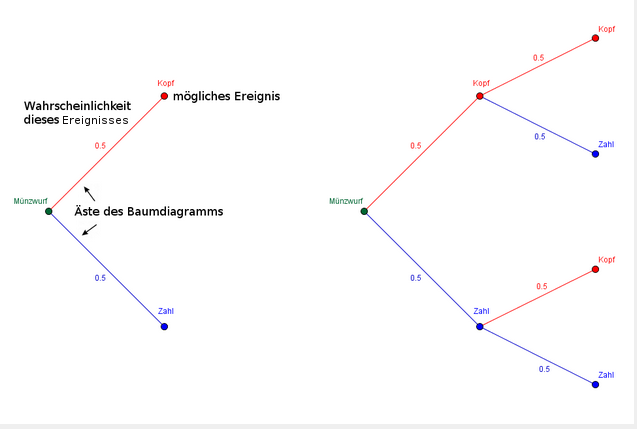
Ein gutes Beispiel für ein einfaches Baumdiagramm lässt sich leicht mithilfe des Münzwurf-Versuchs darstellen. Jedes mögliche Ereignis dieses Zufallsversuchs besitzt eine Wahrscheinlichkeit von $50 \%$.

Baumdiagramm zum Münzwurf

Die sogenannten Äste des Baumdiagramms führen zu den beiden Möglichkeiten Kopf oder Zahl. Auf diesen Ästen steht jeweils die Wahrscheinlichkeit in der Dezimalschreibweise - in diesem Fall ist die Wahrscheinlichkeit bei beiden möglichen Ergebnissen $0,5$.

Nachdem du die Münze einmal geworfen hast, besteht beim zweiten Wurf für jedes Ergebnis, also Kopf oder Zahl, jeweils wieder eine 50%ige Wahrscheinlichkeit. Man schreibt diese zwei neuen Möglichkeiten einfach an jedes Ereignis, dass sich aus dem ersten Wurf ergeben hat, heran.

Wie erstellt man größere Baumdiagramme?

Ergeben sich bei einem Wahrscheinlichkeitsversuch mehr als zwei Möglichkeiten, die dann auch noch unterschiedliche Wahrscheinlichkeiten besitzen, müssen wir ein größeres Baumdiagramm zeichnen, als es noch beim Münzwurf der Fall war.

Betrachten wir ein Beispiel:

Beispiel

Hier klicken zum Ausklappen

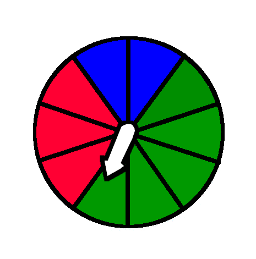
Folgendes Glücksrad wird zweimal hintereinander gedreht. Erstelle ein entsprechendes Baumdiagramm, um die Einzelwahrscheinlichkeiten berechnen zu können.

Glücksrad

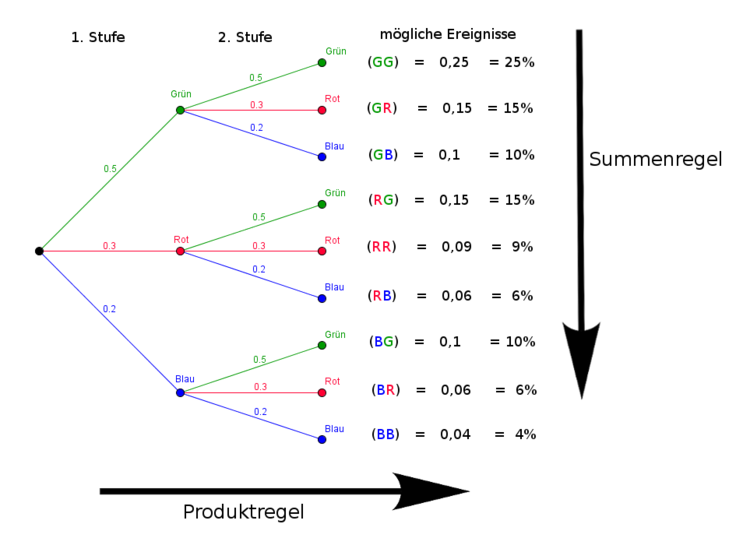
Das entsprechende Baumdiagramm zu dieser Aufgabe sieht folgendermaßen aus:

Baumdiagramm: Zweimaliges Drehen des Glücksrads

Berechnung von Wahrscheinlichkeiten - Produktregel und Summenregel

In der Abbildung erkennst du außerdem, wie die Wahrscheinlichkeiten der einzelnen Kombinationsmöglichkeiten berechnet werden. Dazu musst du einfach die Wahrscheinlichkeiten auf den entsprechenden Pfaden multiplizieren. Dies nennt man auch die Produktregel.

Beispiel

Hier klicken zum Ausklappen

Wir möchten die Wahrscheinlichkeit für die Möglichkeit berechnen, beim ersten Drehen auf einem grünen und beim zweiten Drehen auf einem blauen Feld zu landen. Dazu schauen wir uns den entsprechenden Pfad an:

Einzelner Pfad eines Baumdiagramms.

Um die Wahrscheinlichkeit des Ereignisses "grünes Feld, blaues Feld" zu errechnen, musst du die einzelnen Wahrscheinlichkeiten multiplizieren.

$P (\textcolor{green}{G} \textcolor{blue}{B}) = P(\textcolor{green}{G}) \cdot P(\textcolor{blue}{B})$

$P (\textcolor{green}{G} \textcolor{blue}{B}) = \textcolor{green}{0,5} \cdot \textcolor{blue}{0,2} = 0,1 = 10 \%$

Neben der Produktregel musst du ein weiteres Rechengesetz zur Berechnung von Wahrscheinlichkeiten in Baumdiagrammen kennen: die Summenregel.

Nun hast du viel darüber gelernt, wie du mit Baumdiagrammen Wahrscheinlichkeiten berechnest. Teste dein neu erlerntes Wissen mit unseren Übungsaufgaben! Dabei wünschen wir dir viel Spaß und Erfolg!