Wie berechnet man die Wahrscheinlichkeit von Ergebnissen?

Eines der bekanntesten Wahrscheinlichkeitsexperimente ist der Zufallsversuch. Zufällig sind hierbei die Ergebnisse des Versuchs. In diesem Lerntext werden wir dir das Thema Zufallsversuche erklären und zu diesem Teil der Wahrscheinlichkeitsrechnung Aufgaben mit dir durchgehen. So wirst du dieses Thema schnell verstehen und keine Probleme mehr mit dem Rechnen mit Zufallsversuchen haben.

Wie berechnet man die Wahrscheinlichkeit von Zufallsexperimenten?

Die Berechnung der Wahrscheinlichkeiten der möglichen Ergebnisse folgt einer einfachen Regel.

Zufallsexperimente lösen - Beispielaufgaben

Wahrscheinlichkeit berechnen - Aufgabe 1

Ein typisches Beispiel für einen solchen Zufallsversuch ist das Werfen einer Münze. Wenn eine Münze geworfen wird, sind die möglichen Ergebnisse Kopf oder Zahl. Die jeweilige Wahrscheinlichkeit, dass eines dieser Ergebnisse eintritt, liegt in beiden Fällen bei $50 \%$. Theoretisch ist es auch denkbar, dass die Münze auf der schmalen Kante landet. Dieses extrem unwahrscheinliche Ereignis bleibt in den folgenden Beispielen zur Wahrscheinlichkeitsrechnung ungeachtet.

Wahrscheinlichkeit  = $\frac {Anzahl\ der\ gewünschten\ Ergebnisse}{Anzahl\ aller\ möglichen\ Ergebnisse} = \frac{1}{2} = 0,5 $

Wahrscheinlichkeit berechnen - Aufgabe 2

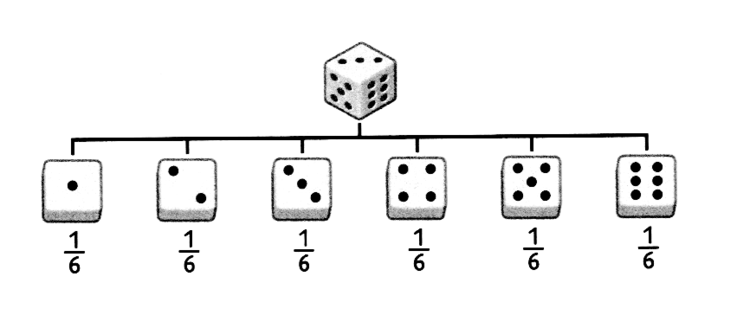
Auch das Werfen eines Würfels ist ein klassischer Zufallsversuch. Ein normaler sechsseitiger Würfel besitzt für jede Seite dieselbe Wahrscheinlichkeit:

Wahrscheinlichkeit  = $\frac {Anzahl\ der\ gewünschten\ Ergebnisse}{Anzahl\ aller\ möglichen\ Ergebnisse} = \frac{1}{6} = 0,1667 = 16,67\%$

Zufallsversuch: Werfen eines Würfels

Was sind Laplace-Versuche?

Was ist eine ungleiche Wahrscheinlichkeit?

Auch wenn es auf den ersten Blick etwas ungewöhnlich wirkt, gibt es auch Zufallsversuche, deren mögliche Ergebnisse nicht gleich wahrscheinlich sind.

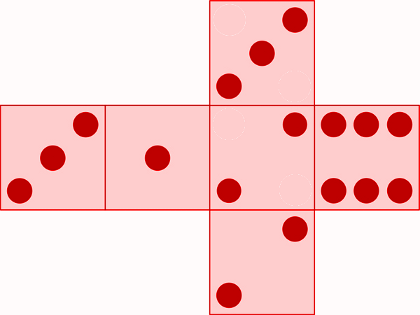
Ein Beispiel wäre ein Würfel, der nicht sechs unterschiedliche Seiten besitzt, wie in diesem Beispiel:

Würfel mit ungleichen Seiten

Wie du siehst, sind nicht alle Zahlen auf diesem Würfel vertreten: die $3$ und die $2$ befinden sich je auf zwei Seiten, wohingegen die $4$ und die $5$ gar nicht vorkommen.

Im Gegensatz zum normalen Würfel sind die Wahrscheinlichkeiten für jedes der möglichen Ergebnisse ($1, 2, 3, 6$) unterschiedlich.

• $P(1) = \frac {1}{6} = 0,1667 = 16,67\%$

• $P(2) = \frac {2}{6} = 0,3333 = 33,33\%$

• $P(3) = \frac {2}{6} = 0,3333 = 33,33\%$

• $P(4) = \frac {0}{6} = 0 = 0\%$

• $P(5) = \frac {0}{6} = 0 = 0\%$

• $P(6) = \frac {1}{6} = 0,1667 = 16,67\%$

Teste dein neu erlerntes Wissen zur Wahrscheinlichkeitsverteilung jetzt mit  Übungsaufgaben! Wir wünschen dir dabei viel Spaß und Erfolg!