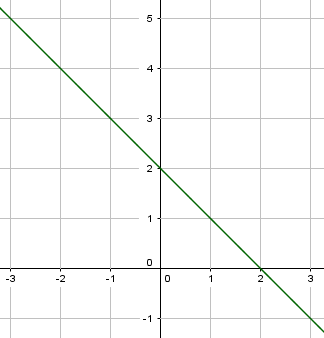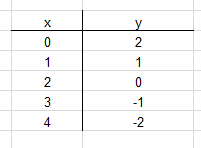Wie erstellt man eine Wertetabelle?

In diesem Kapitel wird dir genau erklärt, wie man in der Mathematik eine Wertetabelle erstellt und wofür man sie am sinnvollsten verwendet. Zudem werden wir mit Hilfe einer Wertetabelle eine Funktion in ein Koordinatensystem einzeichnen.

Was ist eine Wertetabelle?

Wertetabellen findet man vor allem in Verbindung mit einer Funktion. In der Mathematik treten sie also häufiger auf. Es gibt zwei verschiedene Möglichkeiten, wie man mit Wertetabellen umgeht: Entweder, man erstellt anhand einer gegebenen Funktion die Wertetabelle oder man hat eine Wertetabelle gegeben und muss daraus eine Funktion zeichnen.

Wertetabelle erstellen - Funktion aufstellen

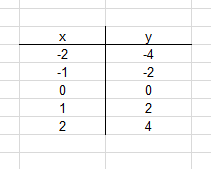
Damit wir mit einer Wertetabelle arbeiten können, müssen wir erst einmal wissen, was genau eine Wertetabelle ist. Hierfür hilft uns die folgende Abbildung:

Beispiel einer Wertetabelle

In der Abbildung sehen wir eine gewöhnliche Wertetabelle. In ihr sind x-Werte und y-Werte eingetragen. Diese Werte sind von Punkten einer Funktion. Du kannst mit diesen Punkten also eine Funktion im Koordinatensystem einzeichnen.

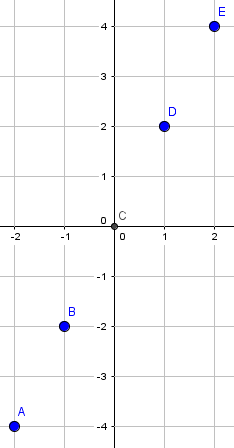
Damit also eine Funktion entstehen kann, bzw. wir den Funktionsgraph auslesen können, müssen wir die Punkte in ein Koordinatensystem eintragen und erhalten dann folgende Abbildung:

eingetragene Punkte aus der Wertetabelle

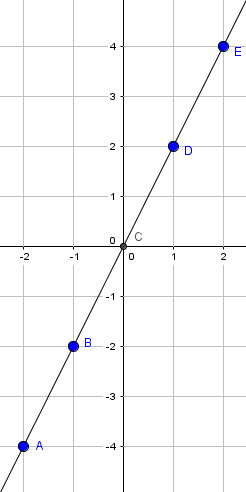
Wenn alle Punkte in das kartesische Koordinatensystem eingetragen sind, dann können wir diese miteinander verbinden und erhalten folgenden Funktionsgraphen:

Verbundene Punkte der Wertetabelle ergeben die Funktion $f(x)=2 \cdot x$

In dieser Abbildung und der dazugehörigen Wertetabelle haben wir die Funktion $f(x)=2 \cdot x$ vorliegen. Mithilfe einer Wertetabelle kann man also die Funktion immer wieder zeichnen, selbst wenn uns die Funktionsgleichung fehlen sollte.

Wie erstellt man eine Wertetabelle bei gegebener Funktion?

Wir können natürlich auch eine Funktion in eine Wertetabelle umwandeln, beziehungsweise durch die gegebene Funktion die dazugehörige Wertetabelle erstellen. Hierfür nehmen wir die Funktion $f(x)= -1 \cdot x + 2$. Diese Funktion bildet auch eine Gerade, hat jedoch eine negative Steigung und auch eine Verschiebung um 2.

Funktionsgraph der Funktion $\textcolor{green}{f(x)= -1 \cdot x + 2}$

Um eine Wertetabelle zu erstellen, zeichnen wir uns erst einmal eine leere Tabelle in der nur x und y im Kopf enthalten sind. Anschließend müssen wir die Wertetabelle ausfüllen, indem wir die wichtigsten Punkte der Funktion in diese Tabelle eintragen. Hierfür sind etwa Schnittstellen mit den Koordinatenachsen interessant. So sieht eine Wertetabelle für die Funktion $f(x)= -1 \cdot x + 2$ aus:

Wertetabelle zur Funktion $f(x)=-1 \cdot x + 2$

Wir erkennen, dass eine Wertetabelle nicht unbedingt die Punkte von $-2$ bis $2$ beinhaltet, so wie in unserer ersten Wertetabelle, sondern sich verschieben kann, je nachdem, wie man es benötigt. Du kannst also selber entscheiden, welche Punkte du in eine Wertetabelle einfügst.

Zur Vertiefung dieses Themas schau auch noch einmal in die Übungen! Dabei wünschen wir dir viel Erfolg und Spaß!