Dreiecke - 6 Arten mit Eigenschaften einfach erklärt
Die geometrische Figur des Dreiecks ist sehr vielseitig. Im folgenden Lerntext erhältst du eine Übersicht über die verschiedenen Dreiecksklassifizierungen und -arten.
Dreieck - Eigenschaften und Aussehen
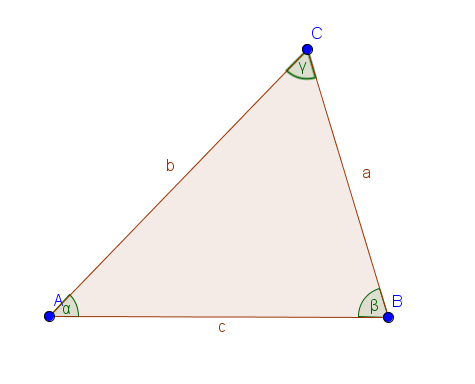
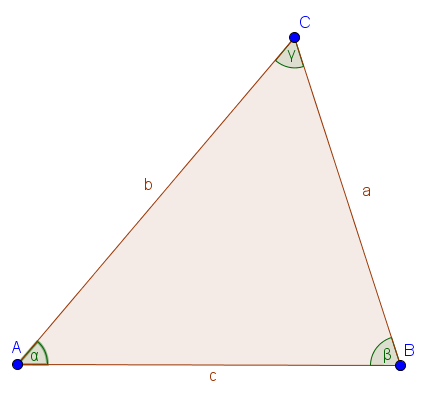
Ein Dreieck besitzt drei Ecken, die mit Großbuchstaben (entgegen dem Uhrzeigersinn) benannt werden. Die Seiten eines Dreiecks werden in Kleinbuchstaben an die ensprechenden Seiten gegenüber der Punkte geschrieben. Außerdem besitzen Dreiecke drei sogenannte Innenwinkel, die mit den griechischen Buchstaben $\alpha$ (Alpha), $\beta$ (Beta) und $\gamma$ (Gamma), entsprechend des Punktes aus dem sie entspringen, bezeichnet werden. Nach dem sogenannten Innenwinkelsatz ergeben alle Winkel eines Dreiecks zusammen $180°$.
In manchen Mathematikbüchern findest du auch folgende Definition: Ein Dreieck ist ein Streckenzug aus drei Strecken.
Hinweis
Innenwinkelsatz: $\alpha + \beta + \gamma = 180°$
Dreiecke können nach den Größen der Seiten oder der Winkel klassifiziert werden.
Klassifizierung von Dreiecken - Die Größe der Seitenlängen
Ungleichseitige Dreiecke sind Dreiecke, deren drei Seiten alle unterschiedlich lang sind.
Merke
Für ein ungleichseitiges Dreieck gilt: $a~\neq~b~\neq~c$
Dreiecke werden als gleichschenklig bezeichnet, wenn zwei der drei Seiten gleich lang sind. Die gleich langen Seiten bezeichnet man als Schenkel, die dritte Seite als Grundseite oder Basis.
Merke
Für gleichschenklige Dreiecke gilt: $a~=~b~\neq~c$
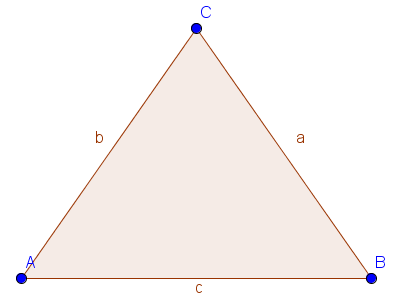
Dreiecke können auch drei gleich lange Seiten besitzten. Man bezeichnet dieses Dreieck dann als gleichseitig. In einem gleichseitigen Dreieck beträgt die Größe jedes Innenwinkels $60°$.
Merke
Für gleichseitige Dreiecke gilt: $a~=~b~=~c$
Klassifizierung von Dreiecken - Die Größe der Winkel
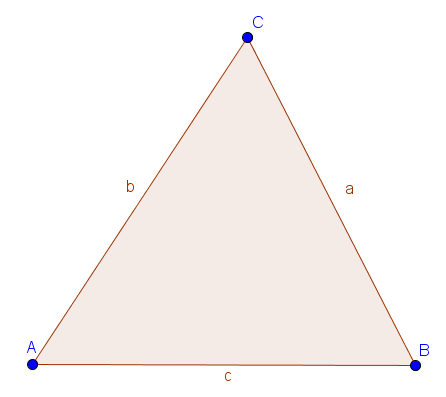
Dreiecke werden als spitzwinklige Dreiecke bezeichnet, wenn sie ausschließlich Winkel unter $90°$ besitzen. Die Seiten können, müssen aber nicht, gleich lang sein.
Merke
Für spitzwinklige Dreiecke gilt: $\alpha < 90°$, $\beta < 90°$, $\gamma < 90°$
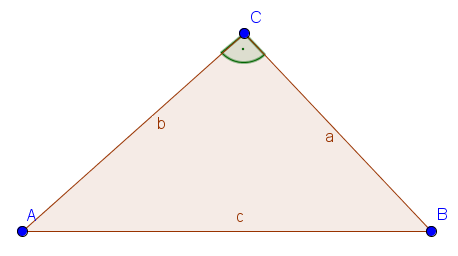
Eine sehr wichtige Dreiecksart ist das rechtwinklige Dreieck. Ein rechtwinkliges Dreieck besitzt einen rechten Winkel. Die Seiten, die die Schenkel des rechten Winkels bilden, nennt man Katheten. Die Seite, die dem rechten Winkel gegenüber liegt, bezeichnet man als Hypotenuse. Die beiden anderen Winkel müssen nach dem Innenwinkelsatz spitze Winkel sein, also unter $90°$. Das rechtwinklige Dreieck wird dir noch oft begegnen zum Beispiel beim Satz des Pythagoras, dem Satz des Thales sowie dem Höhen- und Kathetensatz.
Merke
Für rechtwinklige Dreiecke gilt: $\alpha$ oder $\beta$ oder $\gamma = 90°$
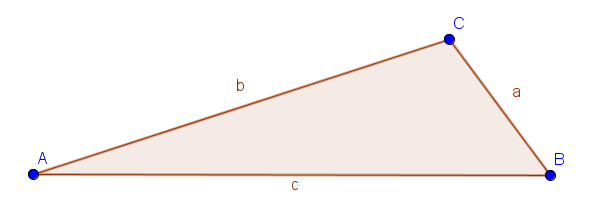
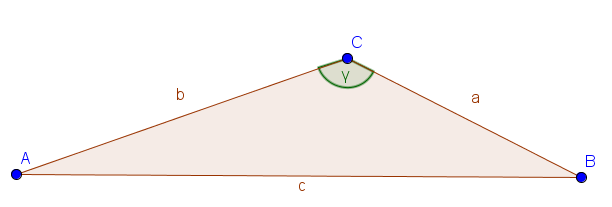
Stumpfwinklige Dreiecke besitzen einen stumpfen Winkel, das heißt einen Winkel zwischen $90°$ und $180°$. Die Seite gegenüber dem stumpfen Winkel ist die längste Seite des Dreiecks.
Merke
Für stumpfwinklige Dreiecke gilt: $\alpha$ oder $\beta$ oder $\gamma = 90°$ bis $180°$
Teste dein neu erlerntes Wissen mit unseren Übungsaufgaben!
Weitere interessante Inhalte zum Thema
-
Gleichgewichtsorgan - Vestibuläre Rezeption
Vielleicht ist für Sie auch das Thema Gleichgewichtsorgan - Vestibuläre Rezeption (Sinnesphysiologie) aus unserem Online-Kurs Neurobiologie interessant.
-
Eigenschaften der Alkanole
Vielleicht ist für Sie auch das Thema Eigenschaften der Alkanole (Organische Verbindungen - Typen, Eigenschaften und Reaktionen) aus unserem Online-Kurs Organische Chemie interessant.