Dreiecke berechnen - Formeln einfach erklärt

In diesem Text erklären wir dir, wie du bei der Dreiecksberechnung vorgehst. Dazu zeigen wir dir an Beispielen, wie du den Umfang und Flächeninhalt eines Dreiecks unter Verwendung bestimmter Formeln berechnen kannst.

Hier erhälst du einen kurzen Überblick zur Flächenberechnung eines Dreiecks:

Eigenschaften eines Dreiecks

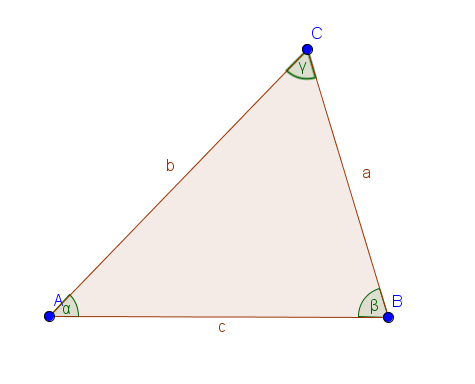
as Ein Dreieck besitzt drei Punkte (Ecken), die in der Regel gegen den Uhrzeigersinn mit Großbuchstaben benannt werden ($A, B, C$). Die drei Seiten des Dreiecks werden mit den entsprechenden Kleinbuchstaben beschriftet. Dabei werden die Seiten nach den gegenüberliegenden Punkten benannt. Gegenüber des Punktes $B$ liegt also beispielsweise die Seite $b$.

allgemeine Darstellung eines Dreiecks

Ebenfalls wichtig sind die Innenwinkel des Dreiecks. Diese werden mit den griechischen Buchstaben $\alpha$ (Alpha), $\beta$ (Beta) und $\gamma$ (Gamma) bezeichnet.

Wie berechnet man den Umfang eines Dreiecks?

Der Umfang des Dreiecks lässt sich sehr einfach berechnen. Er ist die Summe aller Seitenlängen. Es gilt also:

Um den Umfang eines Dreiecks berechnen zu können, müssen alle drei Seitenlängen bekannt sein. Genauso kann es sein, dass der Umfang und zwei Seitenlängen gegeben sind und du die fehlende Seitenlänge berechnen musst. Dazu musst du die Formel umstellen.

Wie berechnet man den Flächeninhalt eines Dreiecks?

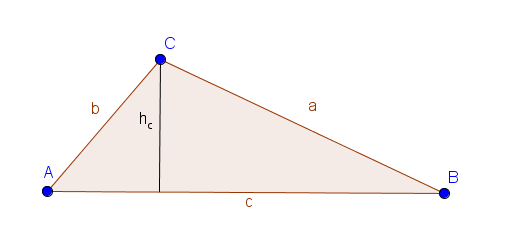
Um den Flächeninhalt eines Dreiecks berechnen zu können, benötigen wir eine weitere Größe: die Höhe. Die Höhe eines Dreiecks ist ein Lot, das von einem Punkt auf die gegenüberliegende Seite gefällt wird. Dementsprechend existieren in einem Dreieck drei unterschiedliche Höhen. Für den Flächeninhalt benötigen wir aber nur eine; in unserem Beispiel die Höhe auf die Seite $c$ ($h_c$).

Dreieck mit Höhe

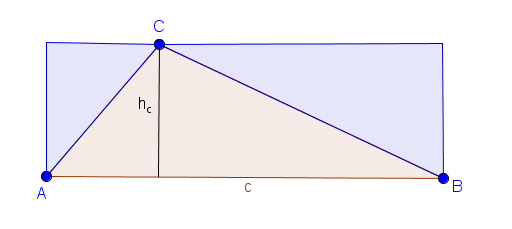
Durch das Einzeichnen der Höhe teilen wir das Dreieck in zwei rechtwinklige Dreiecke. Diese Dreiecke werden nun an ihren längsten Seiten mit einem kongruenten Dreieck ergänzt, das so gedreht wird, dass sich ein Rechteck bildet.

Erweiterung des Dreiecks zum Rechteck

Das Ergänzen der Dreiecke musst du zum Glück nicht jedes Mal aufs Neue machen, um den Flächeninhalt des Dreiecks zu berechnen. Wir erhalten nämlich eine Formel, mit deren Hilfe wir den Flächeninhalt in Zukunft ganz einfach berechnen können. Betrachten wir die geometrische Figur als Ganzes, erhalten wir ein Rechteck mit den Seitenlängen $c$ und $h_c$. Ganz allgemein bezeichnet man $h_c$ als Höhe und $c$ als die Grundseite. Um den Flächeninhalt des Rechtecks zu berechnen, müssen wir die Seitenlängen multiplizieren.

$A_{Rechteck} = g \cdot h =$ Grundseite $\cdot$ Höhe

Diese Formel können wir für unser Dreieck aber nicht einfach übernehmen, da wir uns ja Flächen dazugedacht haben, um ein Rechteck zu bilden. Wir müssen den Flächeninhalt des Rechtecks noch durch $2$ teilen, um auf den Flächeninhalt des Dreiecks zu kommen.

$A_{Dreieck} = \frac{g \cdot h}{2} = \frac{1}{2} \cdot g \cdot h$

Nun kennst du die Dreieck-Formeln für den Umfang und den Flächeninhalt und kannst Berechnungen an einem Dreieck durchführen. Teste dein neu erlerntes Wissen zum Thema Dreieck berechnen online mit unseren Übungsaufgaben! Dabei wünschen wir dir viel Spaß und Erfolg!