Aufstellen und Vereinfachen von Termen einfach erklärt
In diesem Text erklären wir dir, wie du in Mathe Terme aufstellen, vereinfachen und berechnen kannst. Wir erläutern dir die Regeln zum Vereinfachen von Termen und vertiefen später dein neu erlerntes Wissen zum Thema Terme mithilfe der Übungen.
Was sind Terme?
Terme sind mathematische Rechenausdrücke, die einen sinnvollen Zusammenhang beschreiben. Dabei kann es sich um einen Sachverhalt oder um einen Rechenausdruck handeln. Terme bestehen aus Zahlen, Rechenzeichen und oftmals auch aus Variablen.
Beispiel
$(a+2b)\cdot 3$
Variablen kennzeichnen kleine Buchstaben, die für veränderbare Größen stehen.
Merke
Variablen
Variablen kennzeichnen eine veränderbare Größe. Sie werden mit kleinen Buchstaben gekennzeichnet. Oftmals wird $x$ als Symbol verwendet.
Gleichungen haben im Unterschied zu Termen ein Gleichheitszeichen. Somit besteht eine Gleichung aus zwei Termen:
$\textcolor{red}{4x+5} ~= \textcolor{blue}{2x-10}$
$\textcolor{red}{Term 1} =\textcolor{blue}{Term 2}$
$~~~~~~Gleichung$
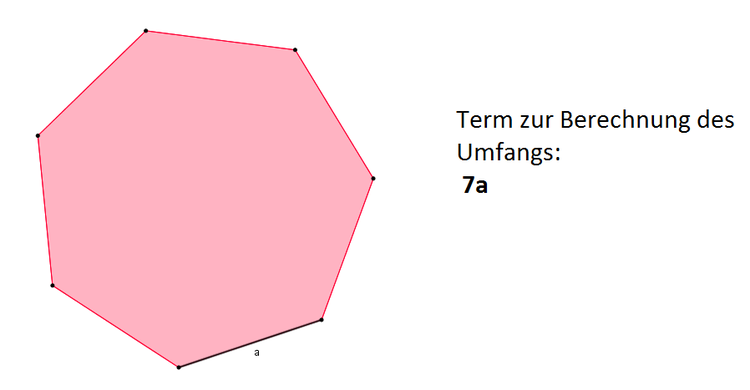
Ein Beispiel für einen Term ist die Formel des Umfangs einer Fläche:
Wie stellt man Terme auf?
Schriftlich beschriebene Rechenvorgänge können in Terme umgeformt werden. Das Aufstellen von Termen ist letztlich nichts weiter als das Umwandeln von Wörtern in mathematische Symbole.
Beispiel
Multipliziere $5$ mit $x$. $\rightarrow~~~5\cdot x$
Halbiere die Summe von $5$ und $7$. $\rightarrow~~~\frac{5+7}{2}$
Subtrahiere die Zahl $20$ von der Differenz der Zahlen $5$ und $55$. $\rightarrow ~~(55-5)-20$
Addiere zum Produkt von $3$ und $15$ das Doppelte von 2. $\rightarrow~~ 3\cdot 15 + 2\cdot 2$
Wie wir sehen, gibt es für bestimmte Ausdrücke ein zugehöriges Rechensymbol.
Addition ($~+~$)
$Summand + Summand= Summe$
addieren, zusammenzählen ...
Subtraktion ($~-~$)
$Minuend - Subtrahend = Differenz$
subtrahieren, Minus-Rechnen, abziehen, Unterschied oder Differenz (größer - kleiner) ...
Division ($~:~$)
$\large{\frac{Divisor}{Dividend}=Quotient}$
teilen, dividieren, halbieren, den Quotienten bilden aus ...
Multiplikation ($~\cdot~$)
$Faktor \cdot Faktor = Produkt$
Mal-Rechnen, vervielfachen, multiplizieren, das Produkt berechnen ...
Wie berechnet man Terme? - 2 Regeln
Es gibt nicht nur Terme, bei denen wir zwei Werte miteinander verrechnen. Es können auch mehr als zwei Zahlen mit verschiedenen Rechenausdrücken und Klammern zusammengerechnet werden. Hierfür werden Rechenregeln benötigt, damit jeder auf dasselbe Ergebnis kommt. Schauen wir uns dazu folgendes Beispiel an:
Beispiel
Häufige Fehler:
$10+(5\cdot 8-17)$
Gehen wir von links nach rechts vor und beginnen mit $10+5$ und verrechnen weiter $15 \cdot 8$. Dies ergibt $120$. Ziehen wir davon $17$ ab, erhalten wir $103$ als Ergebnis. Diese Lösung ist jedoch falsch, da wir die Rechenregeln nicht beachtet haben.
Schauen wir uns zwei wichtige Rechenregeln an:
Merke
Regel 1:
Bei Termen mit Klammern berechnet man zuerst das, was in den Klammern steht.
Merke
Regel 2:
Punktrechnung ($\cdot, :$) kommt vor Strichrechnung ($+, -$).
Hinweis
Eine Eselsbrücke für dich, damit du dir die zwei Rechenregeln oben in Zukunft sehr einfach merken kannst:
Die Klammer sagt: „Zuerst komm ich!“ Denk ferner dran: „Stets Punkt vor Strich“ Und was noch nicht zum Rechnen dran, das schreibt man unverändert an.
Berechnen wir den Term erneut unter Berücksichtigung der Regeln:
Beispiel
$10+(5\cdot 8-17)$
Als erstes muss $5\cdot 8$ gerechnet werden, da dies eine Punktrechnung ist.
$10+(40-17)$
Nun muss der Wert in der Klammer zusammengerechnet werden.
$10+23 = 33$
Damit haben wir das richtige Ergebnis berechnet.
Wie vereinfacht man Terme? - 3 Regeln
Terme können vereinfacht werden! Beim Vereinfachen sollten folgende Punkte beachtet werden:
- Gleichartige Variablen können bei der Additionen und Subtraktionen zusammengefasst werden.
$ a+2a=3a$
$ x + x + x+ 4y -x +y = 2x+5y$ - Bei der Multiplikation werden die Zahlen multipliziert. Die Variablen bleiben als Faktoren vorhanden.
3y · 2z = 3 · y · 2 · z = 6 · y · z = 6yz - Bei der Division kann man gleiche Variablen in Zähler und Nenner kürzen, jedoch nur wenn diese durch Multiplikation verbunden sind.
$\frac{4b}{2b}= \frac{4\cancel{b}}{2\cancel{b}}=\frac{4}{2}=2$
Beispiel
$5x+3 +8+2x$
Dieser Term kann vereinfacht werden! Wir sehen, dass zweimal die Variable $x$ vorkommt und auch zwei Zahlen, die miteinander verrechnet werden können.
$5x+2x = 7x$
$3+8 = 11$
Damit erhalten wir den Term:
$7x +11$
Nun hast du schon viel über das Rechnen in Mathe mit Termen erfahren und kannst Terme aufstellen, Terme vereinfachen und Terme berechnen. Teste dein neu erlerntes Wissen zum Thema Terme Vereinfachen online mit unseren Übungsaufgaben!
Weitere interessante Inhalte zum Thema
-
Extrempunkte kubische Schar
Vielleicht ist für Sie auch das Thema Extrempunkte kubische Schar (Funktionsuntersuchung ganzrationaler Kurvenscharen) aus unserem Online-Kurs Grundlagen der Analysis (Analysis 1) interessant.
-
Gleichungen höheren Grades lösen
Vielleicht ist für Sie auch das Thema Gleichungen höheren Grades lösen (Gleichungen lösen) aus unserem Online-Kurs Vorkenntnisse zur Analysis interessant.