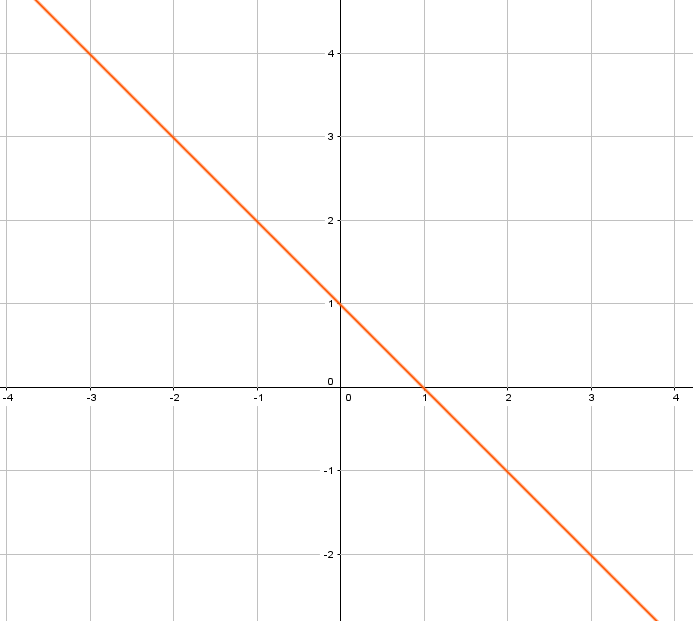Wie bestimmt man die Nullstelle einer linearen Funktion?

In der Analysis ist das Bestimmen der Nullstellen von elementarer Bedeutung. Eine lineare Funktion kann nur eine oder keine Nullstelle haben. Wie man die Nullstelle einer Funktion ablesen bzw. berechnen und ablesen kann, klären wir in diesem Kapitel.

Wie bestimmt man graphisch die Nullstelle einer Funktion? 

Eine Nullstelle ist ein Schnittpunkt mit der $x-Achse$. Also gehen wir ähnlich vor, wie beim Bestimmen des y-Achsenabschnitts. 

Wenn die Abbildung eines Graphen gegeben ist, können wir die Nullstelle einfach ablesen bei der Funktion, solange der Punkt genau erkennbar ist:

Abbildung lineare Funktion mit Nullstelle

Die Nullstelle liegt am Punkt $N(1/0)$. Bei einer Nullstelle ist der $y-Wert$ immer null. $\rightarrow N(x/\textcolor{BrickRed}{0})$. Du hast also gerade gelernt, wie du bei der Funktion die Nullstelle ablesen, also graphisch bestimmen kannst. Natürlich ist dies nicht immer möglich, weswegen es noch ein anderes Verfahren gibt: Du kannst rechnerisch Nullstellen bestimmen.

Wie bestimmt man rechnerisch die Nullstelle einer Funktion?

Die Nullstelle befindet sich dort, wo der $y-Wert$ null ist. Also muss, um den Nullpunkt zu berechnen, die lineare Funktion gleich null gesetzt werden. Schauen wir uns dies rechnerisch an einem Beispiel an:

Nullstelle einer linearen Funktion berechnen - 3 Schritte der Vorgehensweise

3 Beispielaufgaben - Wie bestimme ich die Nullstelle von linearen Funktionen?

Bestimme je die Nullstelle der Funktionen!

a) $f(x) = -0,5 \cdot x + 2 $
b) $g(x) = 50 \cdot x +25$
c) $h(x) = -x-1,75$

a) $f(x) = -0,5 \cdot x + 2 $

1. Die Funktion gleich null setzen
$f(x) = -0,5 \cdot x +2 = 0$

2. nach $x$ auflösen
$0 = -0,5 \cdot x + 2$     $|-2$
$-2 = -0,5 \cdot x$     $|:(-0,5)$
$\frac{-2}{-0,5} = 4 = x$

3. Nullstelle aufschreiben
$N_f(4/0)$

b) $g(x) = 50 \cdot x +25$

$g(x) = 50 \cdot x +25 = 0$     $|-25$

$-25 = 50 \cdot x$     $|:50$

$\frac{-25}{50} = -0,5 = x$

$N_g(-0,5/0)$

c) $h(x) = -x-1,75$

$h(x) = - x - 1,75 = 0$     $|+1,75$

$1,75 = -x$     $|:(-1)$

$-1,75 = x$

$N_h(-1,75/0)$

Gibt es lineare Funktionen ohne Nullstelle?

Jede lineare Funktion hat entweder eine Nullstelle oder keine Nullstelle.

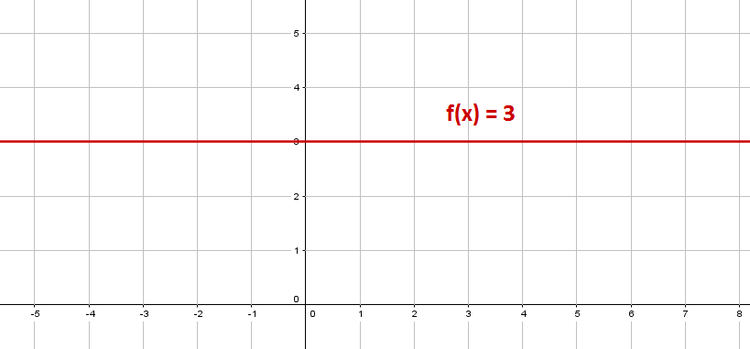
Funktionen, die keine Nullstelle besitzen, verlaufen parallel zur $x-Achse$. 

Abbildung lineare Funktion ohne Nullstelle

Diese Gerade wird die $x-Achse$ nie schneiden.

$f(x) = y= m\cdot x +n \rightarrow$ Die Steigung einer Funktion, die keine Nullstelle besitzt, ist null. $m = 0$
$f(x) = y = 0 \cdot x +3 = 3$
$f(x) = y = 3$

Eine lineare Funktion, die eine Parallele zur $x-Achse$ ist, hat keinen Wert für $x$ bzw. ist er gleich null. Somit gibt es keinen Schnittpunkt mit der x-Achse.

Jetzt weißt du alles Wichtige über das Bestimmen der Nullstelle einer linearen Funktion. Du kannst dich noch weiter mit Hilfe der Übungsaufgaben testen. Viel Erfolg dabei!