Prozentrechnung - richtige Anwendung einfach erklärt
Wir treffen alltäglich auf Prozentangaben. [In diesem Text lernst du, was Prozent überhaupt bedeutet und wie wir in Mathe Prozentrechnung anwenden können. Außerdem besprechen wir mit dir Aufgaben zur Prozentrechnung und erklären dir die Lösungen, damit du fit im Thema Prozentrechnung wirst!
Prozent - Begriffserklärung
Der Begriff Prozent leitet sich vom italienischen pro cento ab und bedeutet von Hundert. Prozente drücken Anteile eines Ganzen aus. Ein Prozent entspricht dabei $\frac{1}{100}$ Anteil eines Ganzen.
Beispiel
$25 \% = \frac{25}{100} =$ 25 von 100 Schülern. (ein Viertel aller Schüler)
$82 \% = \frac{25}{100} =$ 82 von 100 Schülern.
$50 \% = \frac{50}{100} =$ 50 von 100 Schülern. (die Hälfte aller Schüler)
$5 \% = \frac{5}{100} =$ 5 von 100 Schülern.
$100 \% = \frac{100}{100} =$ 100 von 100 Schülern. (alle Schüler)
Die Angabe $100\%$ ist streng genommen kein Anteil mehr, sondern entspricht dem Ganzen. Um herauszufinden, wieviel $1 \%$ einer Zahl ist, musst du diese einfach durch $100$ teilen. Den Zusammenhang zwischen Brüchen und Prozentangaben kannst du noch einmal in unserem Lerntext zum Thema Brüche und Prozente nachlesen.
Merke
Prozente drücken Anteile eines Ganzen aus. Ein Prozent entspricht dabei $\frac{1}{100}$ Anteil eines Ganzen.
$x \% = \frac{x}{100}$
Prozentrechnen: Wie rechnet man Prozent in Dezimalzahl um?
Prozente können also nicht nur in einer Prozentangabe mit Prozentzeichen ausgedrückt werden, sondern auch als Brüche. Diesee Brüche lassen sich wiederum in Dezimalzahlen umrechnen. Um eine Prozentangabe in eine Dezimalzahl umzuwandeln, musst du den Wert durch $100$ teilen und das Prozentzeichen ($\%$) weglassen. Tatsächlich kannst du mit Prozenten oft besser rechnen, wenn sie in eine Dezimalzahl umgewandelt worden sind.
Beispiel
Prozentangaben in Dezimalzahlen umwandeln
$3 \% = \frac{3}{100} = 0,03$
$33 \% = \frac{33}{100} = 0,33$
$12 \% = \frac{12}{100} = 0,12$
$0,75 \% = \frac{0,75}{100} = 0,0075$
$60 \% = \frac{60}{100} = 0,6$
$75,5 \% = \frac{75,5}{100} = 0,755$
Merke
Um eine Prozentangabe in eine Dezimalzahl umzuwandeln, musst du den Wert durch $100$ teilen und das Prozentzeichen ($\%$) weglassen.
Prozentrechnen: Wie rechnet man Dezimalzahl in Prozent um?
Genauso kannst du Dezimalzahlen in Prozentangaben umformen, indem du einfach rückwärts rechnest. Du nimmst den Wert also mit $100$ mal und schreibst das Prozentzeichen wieder dazu.
Beispiel
Dezimalzahlen in Prozentangaben umwandeln
$0,5 \rightarrow 0,5 \cdot 100 = 50 \%$
$0,34 \rightarrow 0,34 \cdot 100 = 34 \%$
$0,94 \rightarrow 0,94 \cdot 100 = 94 \%$
$0,002 \rightarrow 0,002 \cdot 100 = 0,2 \%$
$0,07 \rightarrow 0,07 \cdot 100 = 7 \%$
$1 \rightarrow 1 \cdot 100 = 100 \%$
Merke
Um eine Dezimalzahl in eine Prozentangabe umzuwandeln, musst du den Wert mal $100$ nehmen und das Prozentzeichen ($\%$) dahinter schreiben.
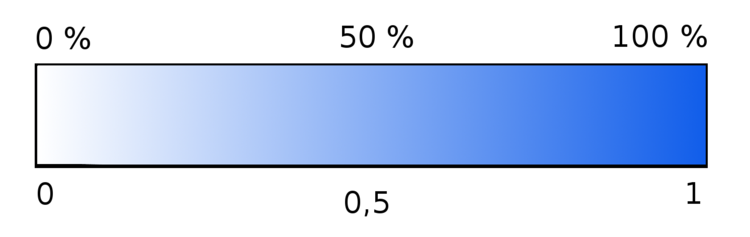
Den Zusammenhang zwischen Prozentangabe und Dezimalzahl kannst du auch nochmal in dieser Abbildung sehen.
Übungen mit Lösungen zur Prozentrechnung
Im Mathematikunterricht werden dir vorallem Textaufgaben zum Thema Prozentrechnung begegnen. Ähnliche wie diese rechnen wir jetzt mit dir durch. Du erhälst dabei Beispielaufgaben mit Lösungen, die dir das Prozentrechnen nochmal vereinfachen werden.
Prozentrechnung: Aufgabe 1
Die Klasse 8b hat 36 Schülerinnen und Schüler. Bei der Wahl zum Klassensprecher erhält Melissa 18 Stimmen. Insgesamt hat die gesamte Klasse 8b abgestimmt. Wie viel Prozent der Klasse haben für Melissa gestimmt?
Lösungsweg
Es haben 36 Schülerinnen und Schüler abgestimmt. Diese Zahl entspricht 100% der Klasse.
Deswegen gilt: $36 Schüler = 100 \%$
Um nun zu berechnen, wie viel Prozent einem Schüler entspricht, gehen wir wie folgt vor:
$1 Schüler = \frac{100}{36} \%$
Da Melissa 18 Stimmen erhalten hat und wir wissen wollen wie viel Prozent der Klasse für Melissa gestimmt haben, gehen wir wie folgt vor:
$18 Schüler = 18 \cdot \frac{100}{36} \% \approx 50\%$
A.: Demnach haben $50 \%$, also die Hälfte der Klasse, für Melissa abgestimmt.
Prozentrechnung: Aufgabe 2
Wegen einer Umleitung fährt Frau Müller eine um 4 km längere Strecke zur Arbeit. Sie fährt jetzt 25 km. Wie viel Prozent mehr fährt Frau Müller jetzt zur Arbeit?
Lösungweg
Im ersten Schritt müssen wir berechnen, wie lang die Strecke zur Arbeit ohne Umleitung war. Das ist nicht schwer. Wir rechnen die 25 km minus der 4 km:
$25-4=21$
Diese 21 km entsprechen also der Strecke zur Arbeit ohne Umleitung und demnach $100 \%$.
Es gilt: $21 km = 100 \%$
Um nun zu berechnen, wie viel Prozent einem Kilometer entspricht, gehen wir wie folgt vor:
$1 km = \frac{100}{21} \%$
Da Frau Müller jetzt 3 km mehr zur Arbeit fährt, berechnen wir im nächsten Schritt, wie viel Prozent diesen 3 km entsprechen:
$3 km = 3 \cdot \frac{100}{21} \% \approx 14,29\%$
A.: Frau Müller fährt wegen der Umleitung $14,29 \%$ mehr Weg zu Arbeit.
Teste dein neu erlerntes Wissen zur Prozentrechnung online mit unseren Übungsaufgaben! Wir wüschen dir viel Erfolg dabei!
Weitere interessante Inhalte zum Thema
-
Klassen
Vielleicht ist für Sie auch das Thema Klassen (Beschreibende Statistik) aus unserem Online-Kurs Stochastik interessant.