Kugelsegment und Kugelausschnitt berechnen - So geht's!
In diesem Lerntext beschäftigen wir uns mit dem Kugelsegment und dem Kugelausschnitt.
Das Kugelsegment - Definition
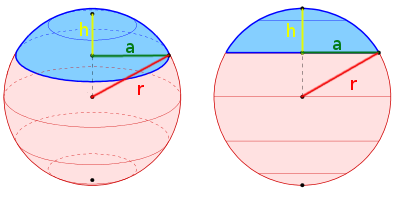
Das Kugelsegment ist der Teil einer Kugel, der entsteht, wenn die Kugel von einer Ebene geschnitten wird. Man könnte auch sagen, dass die Kugel an einer bestimmten Stelle abgeschnitten wird. Das kleine abgeschnittene Stück ist das sogenannte Kugelsegment.
Wie du in der Abbildung sehen kannst, besteht das Kugelsegment aus einer kreisrunden Grundfläche mit einem Radius $a$. Den Radius des Kugelsegments musst du dabei unbedingt vom Radius $r$ der ganzen Kugel, von der das Segment abgeschnitten wurde, unterscheiden. Über dieser Grundfläche spannt sich eine Kuppel, die man auch Kugelhaube nennt. Der größte Abstand zwischen Grundfläche und Kugelhaube ist die Höhe $h$ des Kreissegments.
Hinweis
Die Halbkugel ist eine Sonderform eines Kugelsegments, bei der der Kreismittelpunkt auf der Grundfläche liegt.
Um Volumen und Oberfläche des Kugelsegments zu berechnen, müssen wir die drei genannten Größen ($r$, $a$ und $h$) kennen. Dabei sind diese Größen nicht unabhänngig voneinander, ihr Verhältnis ist durch eine einfache Formel beschrieben:
$r^2 = (r - h)^2 + a^2$
Wie berechnet man die Oberfläche eines Kugelsegments?
Merke
$O_{Kugelsegment} = \pi \cdot (2 \cdot r \cdot h + a^2)$
Beispiel
Berechne die Oberfläche eines Kugelsegments, für das folgendes gilt:
$r ~= 9~cm$
$h ~= 3~cm$
$a ~= 5~cm$
$O_{Kugelsegment} = \pi \cdot (2 \cdot r \cdot h + a^2) = \pi \cdot (2 \cdot 9~cm \cdot 3~cm + 25~cm^2) \approx 248,19~cm^2$
Wie berechnet man das Volumen eines Kugelsegments?
Merke
$V_{Kugelsegment} = \frac{h^2 \cdot \pi}{3} \cdot (3\cdot r - h)$
Beispiel
Berechne das Volumen des oben beschriebenen Kugelsegments.
$V_{Kugelsegment} = \frac{h^2 \cdot \pi}{3} \cdot (3\cdot r - h) = \frac{9~cm^2 \cdot \pi}{3} \cdot (3\cdot 9~cm - 3~cm) \approx 226,176cm^3$
Der Kugelausschnitt - Definition
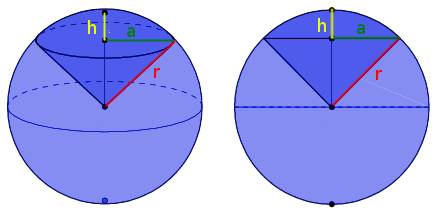
Unter einem Kugelausschnitt versteht man einen kegelförmigen Auschnitt aus einer Kugel, der von der Oberfläche bis zum Mittelpunkt der Kugel geht.
In der zweidimensionalen Betrachtung (rechte Abbildung) sieht man, dass man den Kugelausschnitt in ein Kugelsegment und einen Kegel teilen kann.
Wichtige Größen sind die Höhe $h$ des Kugelsegments, der Radius $a$ der Grundfläche des Kugelsegments und des Kegels sowie der Radius $r$ der gesamten Kugel, der gleichzeitig die Kantenlänge des Kegels ist.
Wie berechnet man die Oberfläche eines Kugelausschnitts?
Merke
$O_{Kugelausschnitt} = \pi \cdot r \cdot (a + 2\cdot h)$
Beispiel
Berechne die Oberfläche für einen Kugelausschnitt, für den gilt:
$r = 8~cm$
$a = 4~cm$
$h = 3~cm$
$O_{Kreisausschnitt} = \pi \cdot r \cdot (a + 2\cdot h) = \pi \cdot 8~cm \cdot (4~cm + 2\cdot 3~cm) \approx 251,33~cm^2$
Wie berechnet man das Volumen eines Kugelauschnittes?
Merke
$V_{Kugelausschnitt} = \frac{2\cdot \pi \cdot r^2 \cdot h}{3}$
Beispiel
Berechne das Volumen des oben beschriebenen Kugelausschnittes.
$V = \frac{2\cdot \pi \cdot r^2 \cdot h}{3} = \frac{2\cdot \pi \cdot 64~cm^2 \cdot 3~cm}{3} \approx 402,12~cm^3$
Teste dein neu erlerntes Wissen über Kugelsegmente und Kugelausschnitte mit unseren Übungsaufgaben! Wir wünschen dir dabei ganz viel Spaß und Erfolg!
Weitere interessante Inhalte zum Thema
-
Extremwertaufgaben (Optimierung)
Vielleicht ist für Sie auch das Thema Extremwertaufgaben (Optimierung) (Differentialrechnung) aus unserem Online-Kurs Weiterführende Aufgaben der Analysis (Analysis 2) interessant.
-
Laplace-Experiment
Vielleicht ist für Sie auch das Thema Laplace-Experiment (Wahrscheinlichkeit) aus unserem Online-Kurs Stochastik interessant.