Volumen/Oberfläche eines Pyramidenstumpfes berechnen
In diesem Lerntext erfährst du alles über den geometrischen Körper des quadratischen Pyramidenstumpfes.
Der Pyramidenstumpf - Merkmale und wichtige Größen
Der Pyramidenstumpf leitet sich vom geometrischen Körper der (quadratischen) Pyramide ab. Die quadratische Pyramide besteht aus einer quadratischen Grundfläche und vier gleichschenkligen Dreiecken als Mantelfläche.
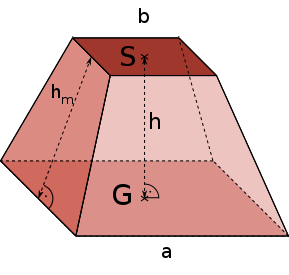
Ein quadratischer Pyramidenstumpf ist wie eine quadratische Pyramide, deren Spitze abgeschnitten wurde. Daraus ergeben sich einige Gemeinsamkeiten und einige Unterschiede im Vergleich zur Pyramide. So besitzt der Pyramidenstumpf eine quadratische Grundfläche $G$ sowie eine quadratische Schnittfläche $S$ und eine Mantelfläche, die aus vier identischen gleichschenkligen Trapezen besteht.
Wichtige Größen im quadratischen Pyramidenstumpf sind außerdem die Höhe $h$ des Stumpfes, die vom Mittelpunkt der Grundfläche zum Mittelpunkt der Schnittfläche geht und die Höhe $h_{m}$ der vier gleichschenkligen Trapeze, die auch als Höhe der Mantelfläche bezeichnet werden kann.
Pyramidenstumpf: Wie berechnet man die Grundfläche und Schnittfläche?
Grund- und Schnittfläche besitzen eine einfache geometrische Form: sie sind quadratisch. Das bedeutet, sie besitzen jeweils vier gleich lange Seiten. Du musst nur darauf achten, dass du die Seitenlänge $a$ der Grundfläche $G$ und die Seitenlänge $b$ der Schnittfläche $S$ nicht verwechselst.
Merke
Grundfläche berechnen
$A_{G} = a^2$
Schnittfläche berechnen
$A_{S} = b^2$
Pyramidenstumpf: Wie berechnet man die Mantelfläche?
Die Mantelfläche besteht aus vier gleichschenkligen Trapezen. Ein Trapez ist ein Viereck mit zwei parallel verlaufenden Seiten, die unterschiedlich lang sind. Bei einem gleichschenkligen Trapez sind zudem die beiden Schenkel gleich lang.
Die Fläche eines Trapez berechnen wir mithilfe dieser Formel:
$A_{Trapez} = \frac{1}{2} \cdot (a + b) \cdot h$
Die Seiten $a$ und $b$ bilden die Unter- und Oberseite des Trapezes. Die Höhe des Trapez entspricht im Pyramidenstumpf der Höhe $h_{m}$ der Mantelfläche. Da die Mantelfläche aus insgesamt vier Trapezen besteht, müssen wir die Gleichung noch mit vier multiplizieren.
Merke
Berechnung der Mantelfläche
$A_{M} = 4\cdot \frac{1}{2} \cdot (a + b) \cdot h_{m} = 2 \cdot (a + b) \cdot h_{m}$
Pyramidenstumpf: Wie berechnet man die Oberfläche?
Die Oberfläche des Pyramidenstumpfes setzt sich zusammen aus der Grundfläche, der Schnittfläche und der Mantelfläche.
Merke
Berechnung der Oberfläche
$O_{Pyramidenstumpf}~= ~A_{Grundfläche}~+~A_{Schnittfläche}~+~A_{Mantelfläche}$
$O_{Pyramidenstumpf}~= ~a^2 ~+~ b^2 ~+~ 2 \cdot (a + b) \cdot h_{m}$
Pyramidenstumpf: Wie berechnet man das Volumen?
Die Formel zur Berechnung des Volumens eines quadratischen Pyramidenstumpfes ist ein wenig komplizierter.
Merke
Volumen berechnen
$V_{Pyramidenstumpf} = \frac{h}{3} \cdot (a^2 + a\cdot b + b^2)$
Teste dein neu erlerntes Wissen zum Pyramidenstumpf mit unseren Übungsaufgaben! Viel Spaß und Erfolg dabei!
Weitere interessante Inhalte zum Thema
-
Rotationsvolumen
Vielleicht ist für Sie auch das Thema Rotationsvolumen (Integralrechnung) aus unserem Online-Kurs Weiterführende Aufgaben der Analysis (Analysis 2) interessant.
-
Extremwertaufgaben (Optimierung)
Vielleicht ist für Sie auch das Thema Extremwertaufgaben (Optimierung) (Differentialrechnung) aus unserem Online-Kurs Weiterführende Aufgaben der Analysis (Analysis 2) interessant.