Mit Höhensatz des Euklid rechnen - Regeln einfach erklärt

Der Höhensatz des Euklid gehört zur Satzgruppe des Pythagoras. Wie der Kathetensatz und der Satz des Pythagoras, befasst sich der Höhensatz mit Berechnungen in rechtwinkligen Dreiecken.

Was berechnet man mit dem Höhensatz?

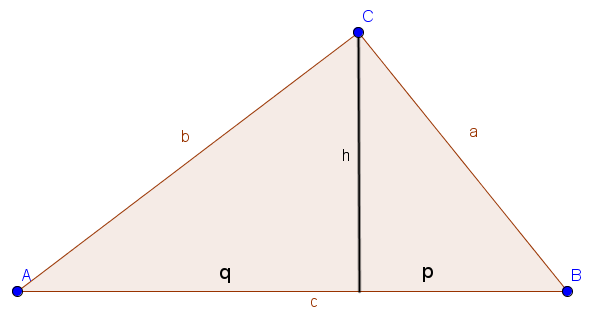
Wie der Name bereits vermuten lässt, benötigen wir die Höhe eines Dreiecks, um den Höhensatz anwenden zu können. Die Höhe eines rechtwinkligen Dreiecks ist ein Lot, das vom Scheitelpunkt des rechten Winkels auf die gegenüberliegende Seite gefällt wird. Die Höhe teilt die Hypotenuse ($c$) in zwei Abschnitte $q$ und $p$.

Dreieck mit Höhe und Hypotenusenabschnitten q und p

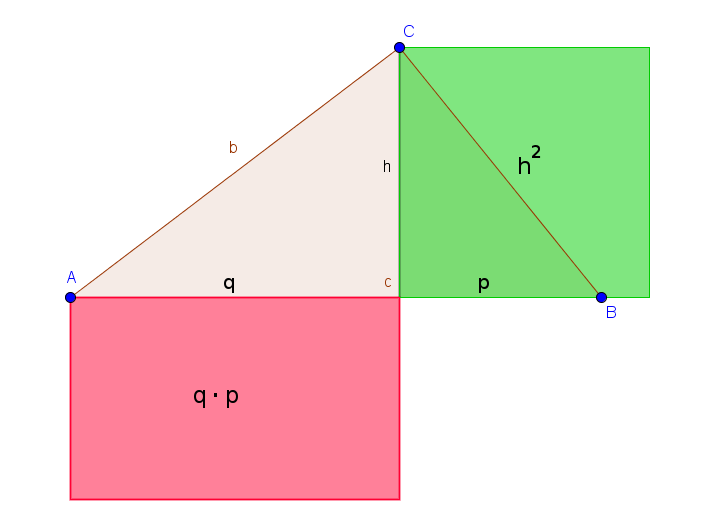
Der Höhensatz bringt die Strecken $q$, $p$ und $h$ in ein Verhältnis. Er besagt, dass das Quadrat der Höhe genauso groß ist wie ein Rechteck mit den Seitenlängen $q$ und $p$.

Höhensatz

Richtig gerechnet? - Beweis des Höhensatzes

Um den Höhensatz zu beweisen, benötigen wir den Satz des Pythagoras sowie die erste binomische Formel.

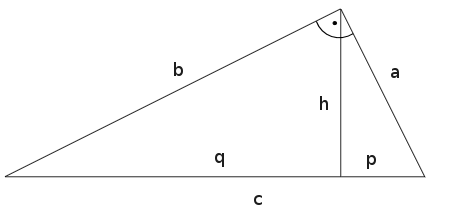
Ein rechtwinkliges Dreieck wird durch das Einzeichnen der Höhe in zwei kleinere, rechtwinklige Dreiecke unterteilt. Insgesamt können wir also drei rechtwinklige Dreiecke erkennen: Ein Dreieck mit den Seitenlängen $a, b, c$, ein Dreieck mit den Seitenlängen $h, p, a$ und ein Dreieck mit den Seitenlängen $h, b, q$.

Rechtwinkliges Dreieck mit Höhe

Jedes dieser Dreiecke ist rechtwinklig und daher können wir jeweils den Satz des Pythagoras anwenden:

1. $\textcolor{blue}{a^2} + \textcolor{red}{b^2} = \textcolor{green}{c^2}$

2. $h^2 + p^2 = \textcolor{blue}{a^2}$

3. $h^2 + q^2 = \textcolor{red}{b^2}$

Außerdem können wir eine weitere Beziehung aufstellen:

• $q + p = c$

Dies lässt sich auch als Quadrat schreiben:

• $(q + p)^2 = c^2$

Mithilfe der ersten binomischen Formel können wir den Klammerterm $(q + p)^2$ auflösen.

$(q + p)^2 = c^2~~~~~|$1. bin. Formel

$q^2 + 2\cdot q \cdot p + p^2 = \textcolor{green}{c^2}$

Diesen neu hergeleiteten Ausdruck für $\textcolor{green}{c^2}$ können wir nun in die 1. Gleichung einsetzen.

$\textcolor{blue}{a^2} + \textcolor{red}{b^2} = \textcolor{green}{c^2}$

$\textcolor{blue}{a^2} + \textcolor{red}{b^2} = q^2 + 2\cdot q \cdot p + p^2$

Außerdem können wir $\textcolor{blue}{a^2}$ und $\textcolor{red}{b^2}$ jeweils durch den linken Term der 2. und 3. Gleichung ersetzen.

$\textcolor{blue}{a^2} + \textcolor{red}{b^2} = q^2 + 2\cdot q \cdot p + p^2~~~~~|h^2 + p^2 = \textcolor{blue}{a^2}$

$h^2 + p^2 + \textcolor{red}{b^2} = q^2 + 2\cdot q \cdot p + p^2~~~~~|h^2 + q^2 = \textcolor{red}{b^2}$

$h^2 + p^2 + h^2 + q^2 = q^2 + 2\cdot q \cdot p + p^2$

Diese neu aufgestellte Gleichung vereinfachen wir nun so weit wie möglich.

$2 \cdot h^2 + p^2 + q^2 = q^2 + 2\cdot q \cdot p + p^2~~~~~|-p^2$

$2 \cdot h^2 + q^2 = q^2 + 2 \cdot q \cdot p~~~~|-q^2$

$2 \cdot h^2 = 2 \cdot q \cdot p~~~~|:2$

$h^2 = q \cdot p$

Nach dem Vereinfachen erhalten wir den Höhensatz des Euklid.

Höhensatz des Euklid anwenden - Beispiel  

Schauen wir uns an einer Beispielrechnung an, wie du den Höhensatz des Euklid anwenden kannst. 

In unserem Beispiel hast du die Höhe $h = 8 cm$ und $q =2 cm$ gegeben. Nun kannst du den Höhensatz $h^2 = p \cdot q$ verwenden, um den fehlenden Wert für $p$ zu berechnen. Dafür setzt du zunächst die gegebenen Werte $h$ und $q$ in die Gleichung des Höhensatzes ein und erhältst: $8^2 = p \cdot 2$.

Im nächsten Schritt löst du die Gleichung mittels Termumformung nach $p$ auf und es ergibt sich folgende Gleichung: $8^2:2=p$. Wenn wir diesen Term nun vereinfachen, ergibt sich $64:2=p$ und das ist 32. Das bedeutet, dass $q$ eine Länge von $32 cm$ hat. 

Um nun noch einmal zu prüfen, ob deine Rechnung stimmt, setzt du $h$, $p$ und $q$ in den Höhensatz ein:

$(8cm)^2=2cm\cdot 32cm$

$64 cm=64 cm$

Da bei deinem Ergebnis auf beiden Seiten der Gleichung ein identisches Ergebnis herauskommt, ist deine Berechnung des Abschnitts $p$ richtig gewesen.

Nun hast du einen detaillierten Überblick über die Herleitung und Anwendungsmöglichkeiten des Höhensatz des Euklid bekommen. Teste dein neu erlerntes Wissen mit unseren Übungsaufgaben! Dabei wünschen wir dir viel Spaß und Erfolg!