Wie löst man lineare Gleichungssysteme zeichnerisch?

Ein lineares Gleichungssystem, auch LGS genannt, besteht aus mindestens zwei linearen Gleichungen. Um lineare Gleichungssysteme zu lösen, können wir neben den rechnerischen Verfahren (Addition, Einsetzen und Gleichsetzen) auch eine zeichnerische Methode benutzen.

Was ist ein Lineares Gleichungssystem? - Definition

Lineares Gleichungssystem zeichnerisch lösen - Schritt für Schritt

Um lineare Gleichungssysteme zeichnerisch zu lösen, gehen wir folgendermaßen vor:

Lineare Gleichungssysteme - Mögliche Lösungsmengen

Wie beim rechnerischen Lösen von linearen Gleichungssystemen, unterscheiden wir auch hier drei unterschiedliche Fälle:

Gleichungssysteme mit einer Lösung

Betrachten wir folgendes Gleichungssystem:

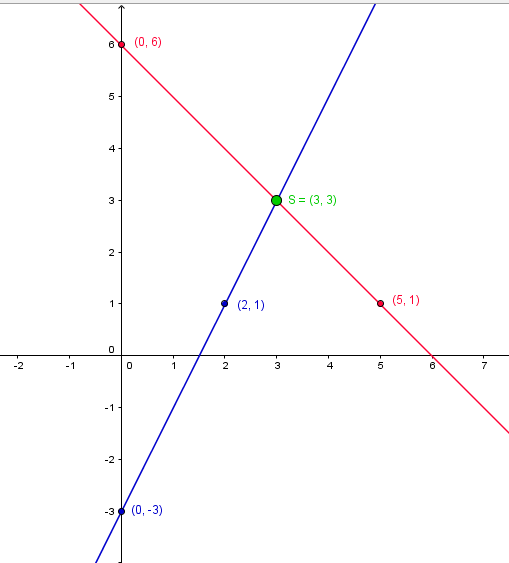
$I: \textcolor{blue}{y= 2\cdot x -3}$

$II:\textcolor{red}{y= - x + 6}$

Die Gleichungen des Gleichungsystems befinden sich schon in der Normalform und wir können direkt jeweils zwei Punkte bestimmen, um die Geraden zu zeichnen.

Lineare Gerade I: Der y-Achsenabschnitt der ersten Gerade liegt bei $\textcolor{blue}{P_1(0|-3)}$. Einen zweiten Punkt erhalten wir, indem wir einen beliebigen x-Wert einsetzen. Wir nehmen beispielsweise den Wert $x = 2$:

$y = 2 \cdot 2 - 3 = 1$

Unser zweiter Punkt lautet demnach $\textcolor{blue}{Q_1(2|1)}$

Lineare Gerade II: Der y-Achsenabschnitt der zweiten Gerade liegt bei $\textcolor{red}{P_2(0|6)}$. Für den zweiten Punkt setzen wir den Wert $x = 5$ ein und erhalten $\textcolor{red}{Q_2(5|1)}$.

Wir bekommen für die beiden Gleichungen also folgende Punkte, die wir einzeichnen und zu Geraden verbinden können.

$\textcolor{blue}{P_1(0|-3)}~;~\textcolor{blue}{Q_1(2|1)}~;~\textcolor{red}{P_2(0|6)}~;~\textcolor{red}{Q_2(5|1)}$

Lineares Gleichungssystem mit einer Lösung

Das Gleichungsystem besitzt eine Lösung, weil sich die Geraden in einem Punkt schneiden. Diesen Punkt können wir ablesen und erhalten die Lösung des Gleichungssystems: $\textcolor{green}{S(3|3)} \rightarrow x =3; y=3$

Am Ende sollten wir unser Ergebnis noch prüfen, indem wir den x- und y-Wert der Lösung in die Gleichungen einsetzen.

$I: 3 = 2\cdot  3 -3 \leftrightarrow 3 = 3~~~~\textcolor{green}{WAHR}$

$II: 3 = - 3 + 6 \leftrightarrow 3 = 3~~~~\textcolor{green}{WAHR}$

Beide Gleichungen ergeben einen wahren Ausdruck. Unser Ergebnis ist also richtig!

Gleichungssysteme ohne Lösung

Schauen wir uns auch hierzu ein Beispiel an:

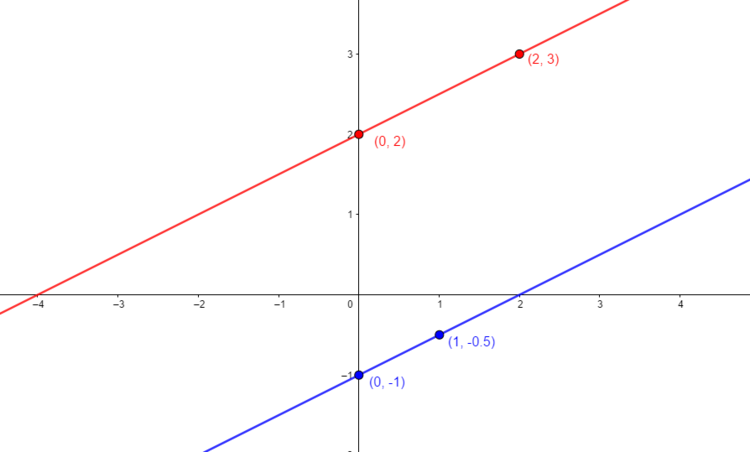
$I: \textcolor{blue}{y= 0,5\cdot x + 2}$

$II:\textcolor{red}{y= 0,5 \cdot x - 1}$

Wir gehen zunächst genauso vor wie im obigen Beispiel und bestimmen jeweils den y-Achsenabschnitt und einen weiteren Punkt, um die Geraden zeichnen zu können. Wir erhalten folgende Punkte:

$I:\textcolor{blue}{P_1(0|2)}~;~\textcolor{blue}{Q_1(2|3)}$

$II: \textcolor{red}{P_2(0|-1)}~;~\textcolor{red}{Q_2(1|-0,5)}$

Zeichnen wir die Geraden in ein Koordinatensystem fällt auf, dass die Geraden keinen Schnittpunkt besitzen. Das Gleichungssystem hat somit auch keine Lösung, die wir ablesen bzw. ausrechnen könnten.

Lineares Gleichungssystem ohne Lösung

Geraden schneiden sich immer dann nicht, wenn sie dieselbe Steigung ,aber einen unterschiedlichen y-Achsenabschnitt besitzen. Die Geraden sind dann Parallelen.

Gleichungssysteme mit unendlich vielen Lösungen

Gleichungssysteme können auch unendlich viele Lösungen besitzen. Das bedeutet, dass die Gleichungen im Gleichungssystem identisch sind. Dies ist oft nicht direkt erkennbar, da die Gleichungen nicht in der Normalform stehen.

Auch in diesem Fall könnten wir die Gleichungen zeichnen, jedoch liegen sie genau aufeinander. Gleichungssysteme besitzen also unendlich viele Lösungen, wenn die Geraden identisch sind.

Teste dein neu erlerntes Wissen zum zeichnerischem Lösen von linearen Gleichungssystemen mit unseren Übungsaufgaben! Viel Erfolg!