Mathematik - Begriffssammlung der 9. Klasse
In diesem Text erhältst du einen Überblick über alle wichtigen Begriffe, die du im Mathematikunterricht der 9. Klasse benötigst. Wir haben die Begriffe nach den verschiedenen mathematischen Oberkategorien (Zahlenlehre und Rechengesetze, Geometrie, Terme und Gleichungen) sortiert.
Möchtest du zu einem dieser Begriffe mehr erfahren, klicke auf die entsprechende Überschrift und du gelangst zur ausführlichen Lernseite zu diesem Thema.
Begriffe zur Zahlenlehre und zu Rechengesetzen
Potenz
Merke
Die Potenz beschreibt einen mathematischen Ausdruck, bei dem eine Zahl mehrmals mit sich selber mal genommen (multipliziert) wird.
Eine Potenz besteht aus einer $\textcolor{blue}{Basis}$ und einem $\textcolor{red}{Exponenten}$: $\textcolor{blue}{a}^\textcolor{red}{n}~=~ \underbrace{\textcolor{blue}{a} \cdot ~~ ... ~~ \cdot \textcolor{blue}{a}}_{\textcolor{red}{n}-mal}$
Zehnerpotenz
Merke
Als Zehnerpotenz bezeichnet man eine Potenz, deren Basis die Zahl $10$ ist.
Begriffe zu Termen und Gleichungen
Quadratische Gleichung
Merke
Die quadratische Gleichung ist eine Gleichung, in der die Variable als Basis einer 2er-Potenz vorkommt ($x^2$). Die allgemeine Form einer quadratischen Gleichung lautet: $a \cdot x^2 ~+~b\cdot x ~+~ c ~=~ 0$
Binomische Formeln
Merke
Mithilfe der binomischen Formeln lassen sich Potenzen einer Summe aus den Zahlen $a$ und $b$ berechnen. Dabei können $a$ und $b$ sowohl positive als auch negative Werte annehmen.
Lineares Gleichungssystem
Merke
Lineare Gleichungssysteme bestehen aus mindestens zwei linearen Gleichungen mit jeweils mindestens zwei Variblen $(x, y)$. Dabei muss der Wert einer Variable für beide Gleichungen gelten.
Koeffizient
Merke
Ein Koeffizient ist ein Faktor, der vor einer veränderlichen Größe, wie beispielsweise einer Variablen ($x$), steht.
Pascalsches Dreieck
Merke
Das Pascalsche Dreieck ist ein in einer Dreiecksform angeordnetes Schema von Zahlen, aus dem die Koeffizienten der binomischen Formeln direkt abgelesen werden können.
Begriffe zur Geometrie
Quader
Merke
Der Quader ist eine dreidimensionale Darstellung eines Rechtecks. Er besteht aus $8$ Ecken und $12$ Kanten und wird von $6$ Rechtecken begrenzt. Die gegenüberliegenden Rechtecke sind deckungsgleich, das heißt sie passen genau aufeinander. Man nennt diese Eigenschaft auch Kongruenz. An jeder Ecke laufen drei Kanten zusammen.
Würfel
Merke
Der Würfel ist eine spezielle Variante eines Quaders, bei dem alle Kanten gleich lang sind. Der Würfel besitzt $8$ Ecken und $12$ Kanten. Außerdem wird er von $6$ deckungsgleichen Quadraten begrenzt.
Zylinder
Merke
Der Zylinder ist ein geometrischer Körper, der aus zwei ebenen, parallelen Kreisflächen und einer Mantelfläche besteht. Die beiden Kreisflächen heißen Grund- und Deckfläche.
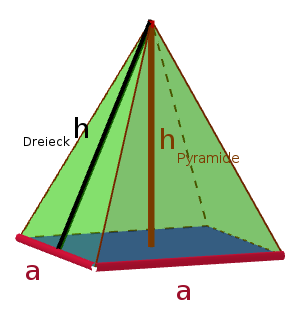
Pyramide
Merke
Die Pyramide besteht aus einem Vieleck als Grundfläche und mehreren gleichseitigen Dreiecken als Mantelfläche, die zu einer Spitze zusammenlaufen. Die Mantelfläche einer Pyramide besitzt genauso viele Dreiecke, wie die Grundfläche Seiten hat.
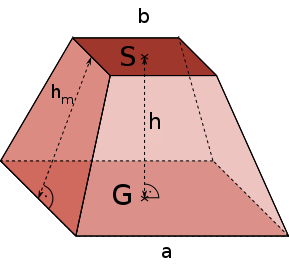
Pyramidenstumpf
Merke
Ein Pyramidenstumpf ist wie eine quadratische Pyramide aufgebaut, deren Spitze abgeschnitten wurde. Er besitzt eine quadratische Grundfläche $G$ sowie eine quadratische Schnittfläche $S$ und eine Mantelfläche, die aus vier gleich großen, gleichschenkligen Trapezen besteht.
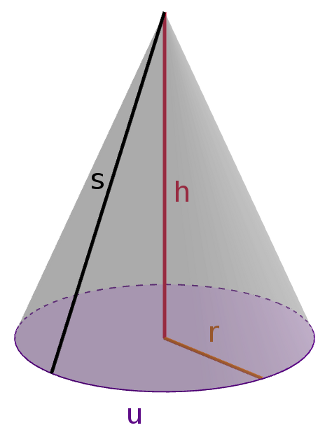
Kegel
Merke
Der Kreiskegel besitzt eine kreisrunde Grundfläche wie der Zylinder und eine Spitze wie die Pyramide. Die Spitze des Kegels befindet sich genau über dem Mittelpunkt der Grundfläche. Die Mantelfläche ist ein Kreisausschnitt.
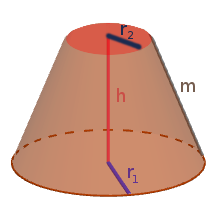
Kegelstumpf
Merke
Ein Kegelstumpf ist ein Kegel, dessen Spitze weggeschnitten wurde. Daraus ergeben sich einige Unterschiede zur ursprünglichen Kegelform. So besitzt der Kugelstumpf neben der für Kegel typischen kreisförmigen Grundfläche auch eine kreisförmige Deckfläche und eine kürzere Kantenlänge. Die Deckfläche wird auch Schnittfläche genannt.
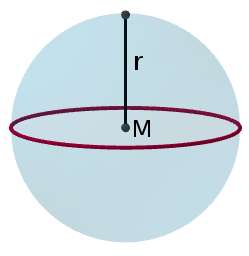
Kugel
Merke
Eine Kugel ähnelt in vielen Punkten der zweidimensionalen Figur des Kreises und besitzt weder Ecken noch Kanten. Die Kugel besteht aus einer Kugelfläche, deren Punkte alle denselben Abstand zum Mittelpunkt $M$ aufweisen.
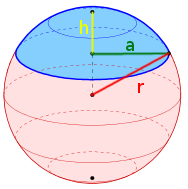
Kugelsegment
Merke
Das Kugelsegment ist der Teil einer Kugel, der entsteht, wenn die Kugel von einer Ebene geschnitten wird. Man könnte auch sagen, dass die Kugel an einer bestimmten Stelle abgeschnitten wird. Das kleine abgeschnittene Stück ist das sogenannte Kugelsegment.
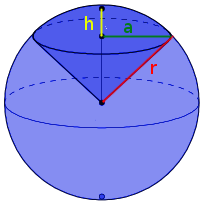
Kugelausschnitt
Merke
Unter einem Kugelausschnitt versteht man einen kegelförmigen Auschnitt aus einer Kugel, der von der Oberfläche bis zum Mittelpunkt der Kugel geht.
Prisma
Merke
Ein Prisma ist ein geometrischen Körper, dessen Grundfläche ein beliebiges Vieleck (z.B. Dreieck, Sechseck) sein kann. Die Seitenkanten sind parallel und gleich lang und die Grund- und Deckfläche somit identisch.
Platonischer Körper
Merke
Ein platonischer Körper ist ein Körper, der aus regelmäßigen Vielecken zusammengesetzt ist. An den Ecken eines platonschen Körpers treffen jeweils gleich viele Vielecke aufeinander.
Zur Vertiefung dieses Wissens schau doch mal in den Übungsaufgaben vorbei! Viel Erfolg dabei!
Weitere interessante Inhalte zum Thema
-
Atomspektren
Vielleicht ist für Sie auch das Thema Atomspektren aus unserem Online-Kurs Atomphysik und Kernphysik interessant.
-
Kernphysikalische Grundlagen und Begriffe
Vielleicht ist für Sie auch das Thema Kernphysikalische Grundlagen und Begriffe (Kernphysik 1) aus unserem Online-Kurs Atomphysik und Kernphysik interessant.