Wie funktioniert das Addieren von Potenzen?
Auf dieser Lernseite beschäftigen wir uns mit der Frage, wie Potenzen einer Summe weiter zusammengefasst werden können.
Addition von Potenzen - Gibt es Rechenregeln?
Die Summe zweier normaler Potenzen, wie sie im unteren Beispiel angegeben sind, lässt sich nicht weiter vereinfachen. Wir können das Ergebnis berechnen, indem wir die einzelnen Potenzen auflösen und dann addieren.
Beispiel
$2^3 + 4^2 = (2 \cdot 2 \cdot 2) + (4 \cdot 4) = 8 + 16 = 24$
Die Summe der Potenzen kann nicht weiter zusammengefasst werden. Um das Ergebnis zu berechnen, rechnen wir die einzelnen Potenzen aus und addieren dann die Potenzwerte.
Potenzen addieren - So geht's!
Die Summe von Potenzen lässt sich nur unter folgenden Voraussetzungen zusammenfassen:
- Die Basen der Potenzen sind gleich.
- Die Exponenten der Potenzen sind gleich.
Sind diese beiden Bedingungen gleichzeitig erfüllt, kannst du die Summe vereinfachen, indem du die Koeffizienten der Potenzen addierst. Als Koeffizient bezeichnet man die Zahl, die als Faktor vor der Potenz steht.
Merke
Die Summe zweier Potenzen kann zusammengefasst werden, indem die Koeffizienten addiert werden.
$\textcolor{blue}{a} \cdot \textcolor{green}{x^n} + \textcolor{red}{b} \cdot \textcolor{green}{x^n} = (\textcolor{blue}{a} + \textcolor{red}{b}) \cdot \textcolor{green}{x^n}$
Addition von Potenzen - Beispiele
Beispiel
$4 \cdot 2^3 + 7 \cdot 2^3 = (4 + 7) \cdot 2^3 = 11 \cdot 2^3 = 88$
$5 \cdot x^3 + 2 \cdot x^3 = (5 + 2) \cdot x^3 = 7 \cdot x^3$
$6 \cdot x^4 + 4 \cdot x^4 = (6 + 4) \cdot x^4 = 10 \cdot x^4$
$3 \cdot x^6 + 5 \cdot x^6 = (3 + 5) \cdot x^6 = 8 \cdot x^6$
Im folgenden Beispiel taucht eine Potenz auf, die auf den ersten Blick keinen Koeffizienten besitzt. Steht vor der Potenz kein Koeffizient, ist der Koeffizient immer die Zahl $1$.
$ x^7 + x^7 = 1\cdot x^7 + 1\cdot x^7 = (1 + 1) \cdot x^7 = 2 \cdot x^7$
$3 \cdot x^3 + x^3 = 3\cdot x^3 + 1\cdot x^3 = (3 + 1) \cdot x^3 = 4 \cdot x^3$
$2 \cdot x^5 + 4 \cdot x^5 + x^5 = 2 \cdot x^5 + 4 \cdot x^5 + 1 \cdot x^5$
$= (2 + 4 + 1) \cdot x^5 = 7 \cdot x^5$
Zusammenfassen der Summen von Potenzen - Wann geht es nicht?
1. Potenzen mit unterschiedlichen Exponenten
$4^\textcolor{red}{5} + 4^\textcolor{red}{6}$
$a^\textcolor{red}{m} + a^\textcolor{red}{n} ~~~~ \rightarrow{\textcolor{red}{NICHT~MOEGLICH}}$
2. Potenzen mit unterschiedlichen Basen
$\textcolor{red}{5}^2 + \textcolor{red}{3}^2$
$\textcolor{red}{a}^n + \textcolor{red}{b}^n ~~~~ \rightarrow{\textcolor{red}{NICHT~MOEGLICH}}$
3. Potenzen mit unterschiedlichen Exponenten und unterschiedlichen Basen
$\textcolor{red}{3}^\textcolor{orange}{4} + \textcolor{red}{9}^\textcolor{orange}{3}$
$\textcolor{red}{a}^\textcolor{orange}{n} + \textcolor{red}{b}^\textcolor{orange}{m} ~~~~ \rightarrow{\textcolor{red}{NICHT~MOEGLICH}}$
Teste dein neu erlerntes Wissen zum Addieren von potenzen mit unseren Übungsaufgaben! Wir wünschen dir dabei viel Spaß und Erfolg!
Weitere interessante Inhalte zum Thema
-
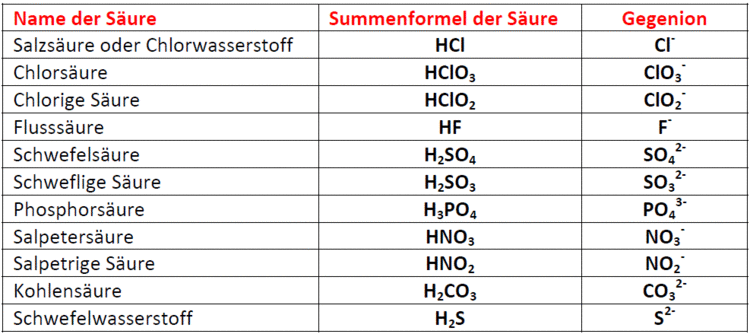
Definition: Säuren und Basen
Vielleicht ist für Sie auch das Thema Definition: Säuren und Basen (Donator-Akzeptor-Prinzip) aus unserem Online-Kurs Anorganische Chemie interessant.
-
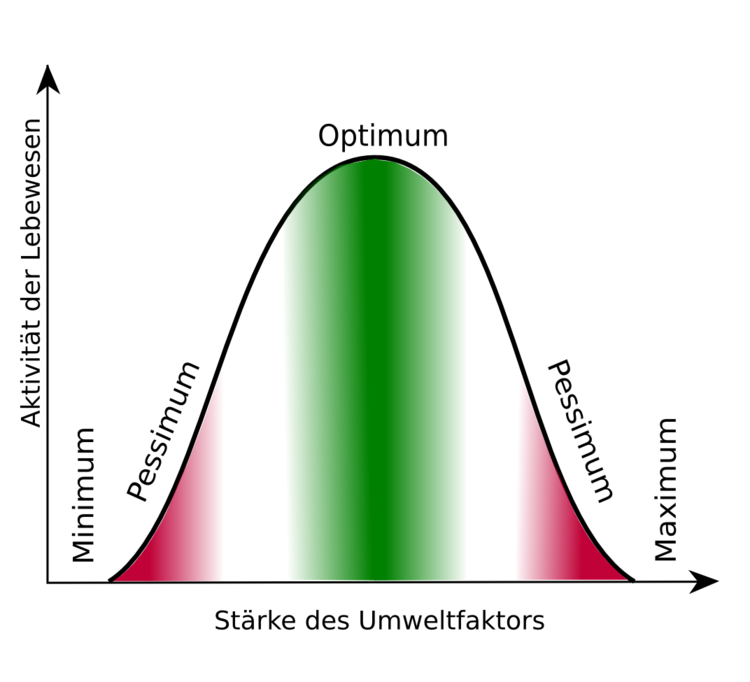
Physiologische und ökologische Potenz
Vielleicht ist für Sie auch das Thema Physiologische und ökologische Potenz (Was ist Ökologie? Grundlegende Regeln im Haushaltsspiel der Natur) aus unserem Online-Kurs Ökologie interessant.