Formeln der Winkelfunktionen Sinus, Cosinus und Tangens
In diesem Text behandeln wir die Winkelfunktionen und zeigen sowie erklären dir die Formeln zu Sinus, Cosinus und Tangens. In der Mathematik werden die Winkelfunktionen der Trigonometrie zugeordnet. Somit gehören die Winkelfunktionen zur Geometrie.
Hier kannst du übersichtlich die drei Winkelfunktionen der Trigonometrie kennenlernen.
Formeln von Sinus, Kosinus, Tangens - Übersicht
Das sind die Formeln der 3 Winkelfunktionen in der Mathematik, die du am besten auswendig lernst.
Merke
- $sin(\alpha) = \frac{Gegenkathete}{Hypotenuse}$
- $cos(\beta) = \frac{Ankathete}{Hypotenuse}$
- $tan(\gamma) = \frac{Gegenkathete}{Ankathete}$
Wie heißen die Seiten, die den rechten Winkel einschließen? - Benennung der Katheten
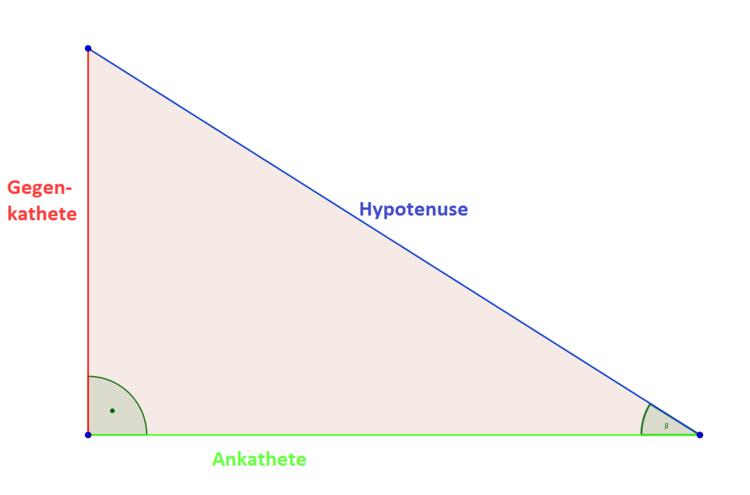
Als Katheten bezeichnet man die beiden Seiten, die den rechten Winkel in einem rechtwinkligen Dreieck einschließen. Die Seite, die gegenüber des rechten Winkels liegt, bezeichnet man als Hypotenuse.
Folgend ein Beispiel:
Die Gegen- und Ankathete beziehen sich immer auf einen Winkel. In unserem Beispiel auf den Winkel $\beta$. Die Gegenkathete liegt gegenüber von $\beta$ und die Ankathete grenzt an $\beta$. Die Hypotenuse liegt immer gegenüber vom rechten Winkel.
Je nachdem, welche zwei Größen gegeben sind und welche Größe gesucht ist, musst du entweder Sinus, Cosinus oder Tangens mit ensprechender Formel anwenden.
Textaufgaben zu Sinus, Kosinus und Tangens lösen - Vorgehensweise
Methode
- Suche das Dreieck und bilde einen rechten Winkel, falls keiner gegeben ist.
- Was ist gesucht und was ist gegeben? Markiere dir dies in einer kleinen Skizze.
- Benenne dann die Katheten.
- Mit der Skizze kannst du nun überlegen, mit welcher Winkelfunktion du arbeiten kannst.
- Als letztes musst du die Werte in die Winkelfunktion einsetzen, gegebenenfalls die Formel umstellen und dein Ergebis dann ausrechnen.
Wichtig ist, dass der Winkel, der gegeben oder gesucht ist, kleiner als $90 ^\circ$ sein muss. Dies ergibt sich aus der Innenwinkelsumme eines Dreiecks. Alle Winkel zusammen, in jedem beliebigen Dreieck, ergeben zusammen $180 ^\circ$. In einem rechtwinkligen Dreieck ist der rechte Winkel $90 ^\circ$ groß. Das bedeutet, die beiden anderen Winkel müssen zusammen $90 ^\circ$ betragen, das heißt, diese beiden Winkel sind jeweils kleiner als $90 ^\circ$.
Nun kennst du die Formeln der Winkelfunktionen in der Geometrie. Teste dein neu erlerntes Wissen jetzt mit unseren Übungsaufgaben!
Weitere interessante Inhalte zum Thema
-
Gleichgewichtsorgan - Vestibuläre Rezeption
Vielleicht ist für Sie auch das Thema Gleichgewichtsorgan - Vestibuläre Rezeption (Sinnesphysiologie) aus unserem Online-Kurs Neurobiologie interessant.
-
Vektoren und Winkel
Vielleicht ist für Sie auch das Thema Vektoren und Winkel (Weitere Rechenoperationen mit Vektoren) aus unserem Online-Kurs Analytische Geometrie / Lineare Algebra (Agla) interessant.