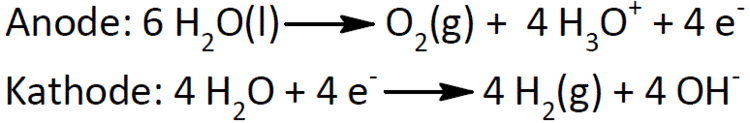abiweb
online lernen

Die perfekte Abiturvorbereitung

Primfaktorzerlegung - Wie berechnet man Primfaktoren?

Zahlenlehre und Rechengesetze / Teilbarkeitslehre

Das Bilden der Primfaktoren, also das Zerlegen von Zahlen, ist ein wesentlicher Bestandteil der Mathematik. In diesem Kapitel findest du eine Erklärung der Begriffe Primfaktor oder Primzahl und Primfaktorzerlegung oder Primzahlzerlegung. Du lernst außerdem, wofür sie verwendet werden können. Das Ganze gehen wir mit einer Übungsaufgabe für ein besseres Verständnis durch.

Wie funktioniert die Primfaktorzerlegung?

Sehr viele Zahlen in der Mathematik können wir in eine Multiplikation von kleineren Zahlen zerkleinern. So auch bei der Zahl $20$. Diese können wir als $2 \; \cdot 10$ schreiben oder noch weitergehen und die $10$ zerkleinern. Diese Zerkleinerung nennen wir in der Mathematik Primfaktorzerlegung oder Primzahlzerlegung. Die einzelnen Zahlen, die am Ende einer Primfaktorzerlegung übrig bleiben, sind nur noch Primzahlen, also Zahlen, die nicht mehr kleiner gemacht werden können, so auch die $2$. Wir nennen sie, wenn sie Teil einer Primfaktorzerlegung sind, dann Primfaktoren.

Merke

Hier klicken zum Ausklappen

Primfaktoren sind nicht weiter zerlegbare Zahlen. 

Die Primfaktorzerlegung zerteilt Zahlen in die Multiplikation mehrerer kleinerer Zahlen.

Dieses Wissen greifen wir jetzt in einem Beispiel auf und zeigen dir, wie man Primfaktoren berechnen kann:

Beispiel

Hier klicken zum Ausklappen

Zerlege die Zahl $64$ in ihre Primfaktoren.

Um die Zahl $64$ zu zerlegen, schaust du der Reihe nach, durch welche natürlichen Zahlen die Zahl $64$ teilbar ist, beginnend bei der $2$. Die Zahl ist durch $2$ teilbar und es entsteht die erste Zerlegung: $2\cdot 32$.

Diesen Schritt wiederholen wir so lange, bis die Zahl komplett zerlegt ist:

$2 \cdot 2 \cdot 16$.

$2 \cdot 2 \cdot 2  \cdot 8$.

$2 \cdot 2 \cdot 2 \cdot 2 \cdot 4$.

$2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2$. Die Zerlegung der Zahl $64$ ist also $2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2$.

Es gibt auch Zahlen, die lassen sich nicht so schön in ihre Primfaktoren zerlegen wie das Beispiel oben. Schon die Zahl $65$ kann nur einmal zerteilt werden, in die beiden Faktoren $5$ und $13$. Weiter lässt sich die Zahl nicht zerteilen.

Primzahlzerlegung - Wie legt man eine Primfaktorentabelle an?

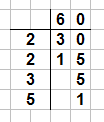
Um eine Zahl in ihre Primfaktoren zu zerlegen und es auch noch optisch zu verschönern, kannst du auch eine Zerlegungstabelle erstellen. Bei dieser wird die Zahl Schritt für Schritt zerlegt, bis auf der linken Seite der Tabelle alle Zerlegungsfaktoren in aufsteigender Reihenfolge stehen. In der Abbildung sehen wir die Zerlegungstabelle der Zahl $60$.

Zerlegungstabelle der zahl 60
Zerlegungstabelle der Zahl $60$.

Wie du erkennst, zerlegt man in der Zerlegungstabelle die Zahlen Stück für Stück und erhält so in der linken Spalte die Primfaktoren. Die Zahl $60$ hat also die Primfaktoren $2,2,3$ und $5$.

Zur Vertiefung dieses Themas schau auch noch einmal in die Übungsaufgaben zur Primfaktorzerlegung! Viel Erfolg dabei!