Tangentengleichung aufstellen - 5 Schritte einfach erklärt
In diesem Lerntext beschäftigen wir uns mit einer Tangente, die an einer Funktion anliegt.
Was ist eine Tangente? - Definition
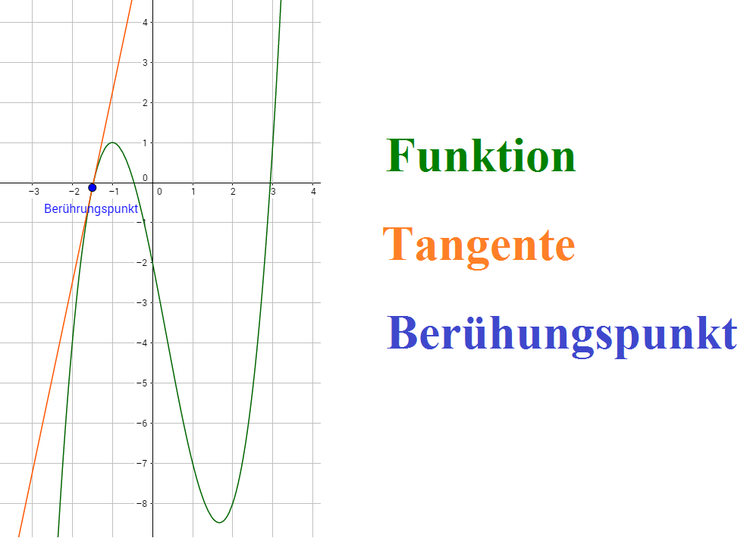
Eine Tangente ist eine Gerade, die einen Funktionsgraphen an einem Punkt berührt. Dabei ist die Steigung der Tangente die Gleiche wie die Steigung des Berührungspunktes.
Eine Tangente ist eine Gerade und besitzt somit die Gleichung einer linearen Funktion.
Hinweis
Der Name Tangente kommt von dem lateinischen Wort tangere, was berühren bedeutet.
Wir schauen uns jetzt an, wie man Tangentengleichungen bestimmen kann:
Wie bestimmt man eine Tangentengleichung? - Vorgehensweise
Meist ist die Funktion und ein x-Wert gegeben, an dem die Tangente anliegen soll. Eine Tangentengleichung bzw. die Gleichung einer linearen Funktion sieht allgemein so aus:
Hinweis
Tangentengleichung
$f(x) = \textcolor{red}{m}\cdot x + \textcolor{blue}{n}$
$\textcolor{red}{m: Steigung}$
$\textcolor{blue}{n: y-Achsenabschnitt}$
Um die Tangentengleichung zu bestimmen, müssen wir den Wert für die Steigung ($m$) und den Wert für den y-Achsenabschnitt ($n$) herausfinden.
Die Steigung ermitteln wir, indem wir den x-Wert in die erste Ableitung einsetzen. Dann müssen wir noch den y-Achsenabschnitt berechnen. Dafür setzen wir den x-Wert und y-Wert des Berührungspunktes und die Steigung in die Tangentengleichung ein und lösen sie nach $n$ auf.
Hier ist die Vorgehensweise nochmal dargestellt:
Methode
Vorgehensweise Tangente berechnen:
- Den x-Wert in die Funktionsgleichung einsetzen, um den dazugehörigen y-Wert zu bestimmen.
- Die Funktion ableiten.
- Den x-Wert in die Ableitung einsetzen und ausrechnen. $\rightarrow$ Wir erhalten die Steigung.
- Die Werte in die allgemeine Gleichung einer linearen Funktion einsetzen und nach $n$ auflösen. $\rightarrow$ Wir erhalten den y-Achsenabschnitt.
- Die Tangentengleichung notieren.
Schauen wir uns dies an einem Beispiel an:
Wie bestimmt man eine Tangentengleichung? - Beispielaufgabe
Beispiel
Die Funktion $f(x) = 2x^2-6x+4$ wird von einer Tangente an der Stelle $x=3$ berührt. Bestimme die Tangentengleichung!
1. Wir berechnen den dazugehörigen y-Wert:
$f(3) = 2\cdot 3^2-6\cdot 3+4 = 4$
Der Berührungspunkt ist $P_B(3/4)$
2. Die Funktion wird abgeleitet:
$f(x) = 2x^2-6x+4$
$f'(x) = 4x-6$
3. Um die Steigung an der Stelle $x=3$ zu ermitteln, setzen wir den Wert in die Ableitung ein. Damit erhalten wir die Steigung an der Stelle $x=3$.
$m = f'(3) = 4\cdot 3-6 = 6~~~\rightarrow~~~ \textcolor{red}{m=6}$
An der Stelle $x=3$ hat die Funktion also eine Steigung von ${m=6}$. Willst du nun die Tangentensteigung berechnen, hast du es jetzt leicht. Denn die Steigung eines Graphen in einem Punkt ist gleich der Steigung der Tangente an dem Graphen in diesem Punkt, also auch ${m=6}$.
4. In die allgemeine Gleichung einer Tangente, $t(x) = m \cdot x +n$, setzen wir die zuvor berechneten Werte ein.
$t(x) = 6 \cdot 3 +n = 4$
$18 +n = 4 ~~~~~~|-18$
$\textcolor{blue}{-14 = n}$
5. Setzen wir die Steigung und den y-Achsenabschnitt in die allgemeine Gleichung ein, dann erhalten wir die Tangentengleichung:
$t(x) =\textcolor{red}{ 6} \cdot x \textcolor{blue}{-14}$
Nun hast du gelernt, wie du eine Tangentengleichung aufstellen kannst. Mit den Übungsaufgaben kannst du dein Wissen überprüfen und anwenden. Viel Erfolg dabei!
Video: Simon Wirth
Text: Chantal Rölle
Weitere interessante Inhalte zum Thema
-
Tangenten- und Normalengleichungen
Vielleicht ist für Sie auch das Thema Tangenten- und Normalengleichungen (Differentialrechnung) aus unserem Online-Kurs Weiterführende Aufgaben der Analysis (Analysis 2) interessant.
-
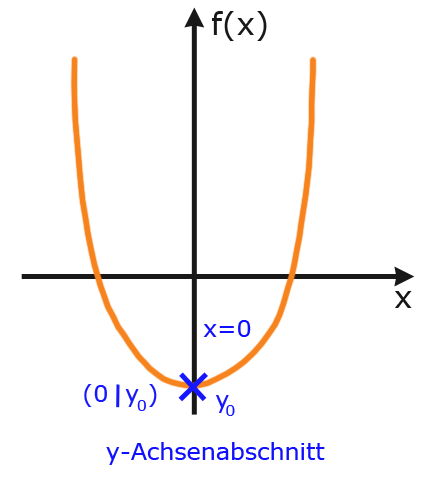
y-Achsenabschnitt
Vielleicht ist für Sie auch das Thema y-Achsenabschnitt (Funktionsuntersuchung ganzrationaler Funktionen Teil 1) aus unserem Online-Kurs Grundlagen der Analysis (Analysis 1) interessant.