Negativer Exponent in Potenzfunktionen

In diesem Lerntext beschäftigen wir uns mit Potenzfunktionen mit einem negativen Exponenten. Hier lernst du die Eigenschaften dieser Funktionen kennen und kannst in den Übungsaufgaben dein Wissen testen. 

Negativer Exponent - 2 Varianten

Eine Funktionsart der Potenzfunktionen sind Potenzfunktionen mit negativem Exponenten. Diese unterscheiden sich in ihren Eigenschaften von den Potenzfunktionen mit natürlichem Exponent. Eine Abbildung verdeutlicht dies am besten:

Potenzfunktion: $f(x)=x^{-4}$

Gerader negativer Exponent

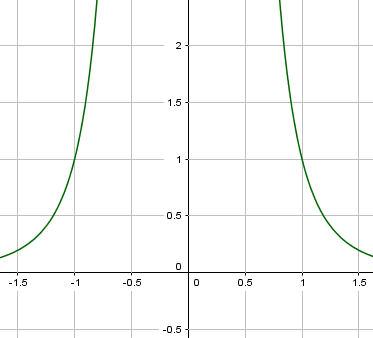
Wir erkennen sofort die großen Unterschiede zur Funktion $f(x)= x^2$. Bei der Funktion oben in der Abbildung ist der Bereich für $x = 0$ nicht definiert, das heißt, x kann nicht Null sein. Du kannst für x eine sehr kleine negative Zahl oder eine sehr kleine positive Zahl einsetzen, aber niemals die Zahl Null. Je dichter der x-Wert, den du in die Funktionsgleichung einsetzt, an der Zahl Null liegt, desto größer wird dein y-Wert. Und je größer der x-Wert (bzw. kleiner bei negativen Zahlen), den du in die Funktionsgleichung einsetzt, desto kleiner wird dein y-Wert. Wir nennen dieses Verhalten, wenn sich eine Funktion sehr stark einem Wert annähert, in der Mathematik Grenzwertverhalten, wobei dieses Verhalten immer durch Asymptoten dargestellt wird. Die beiden Asymptoten für die Funktion in der Abbildung oben sind die x- und die y-Achse. 

Auch haben solche Funktionen in ihrer allgemeinen Form, also ohne Verschiebung entlang der x- oder y-Achse, keine Nullstelle.

Es gibt aber trotzdem Gemeinsamkeiten mit den Potenzfunktionen mit geradem positivem Exponenten. So sind beide Funktionsarten achsensymmetrisch zur y-Achse. Auch haben die Funktionen die Punkte P₁(-1|1) und P₂(1|1) gemeinsam. 

Ungerader negativer Exponent

Etwas anders sieht es bei Potenzfunktionen mit ungeradem negativem Exponenten aus. Diese haben teilweise die Eigenschaften der Potenzfunktionen mit ungeraden positiven Exponenten, sehen jedoch anders aus:

Potenzfunktion: $f(x)=x^{-3}$

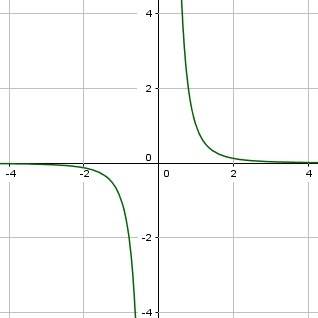
Wir erkennen auch hier die zwei Asymptoten, die x- und die y-Achse, genauso wie den Definitionsbereich, der x = 0 ausschließt. Potenzfunktionen mit einem ungeraden negativen Exponenten gehen alle durch die Punkte P₁(-1|-1) und P₂(1|1), sind also alle punktsymmetrisch zum Koordinatenursprung. Ferner liegen die Graphen solcher Funktionen auch hier wieder nur im ersten und dritten Quadranten des Koordinatensystems.

Potenzfunktionen mit negativem Exponenten - Übungsaufgaben

Jetzt hat du eine detaillierte Übersicht über die Potenzfunktionen mit negativen Exponenten erhalten. Ob du alles verstanden hast, kannst du nun anhand unserer Übungen testen. Dabei wünschen wir dir viel Spaß und Erfolg!