Potenzfunktionen - Aufstellen der Umkehrfunktion

In diesem Text erklären wir dir, was die Umkehrfunktion einer Potenzfunktion ist und wie du sie berechnen kannst.

Was ist eine Umkehrfunktion? - Definition

Umkehrfunktionen ordnen, wie der Name schon sagt, die Funktion umgekehrt zu. Das bedeutet, dass der $x$-Wert mit dem $y$-Wert getauscht wird. Dies ist nur möglich, wenn es für jeden Funktionswert $(y)$ nur einen $x$-Wert gibt.

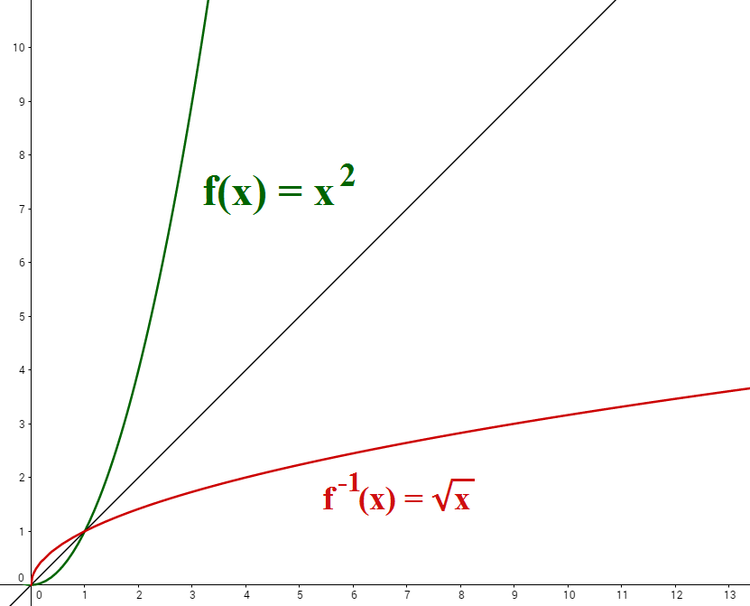
Grafisch kannst du die Umkehrfunktion bilden, indem du die Funktion an der Winkelhalbierenden, also an der Funktion $f(x) =x$, spiegelst.

Umkehrfunktion bilden

Die Umkehrfunktion der Funktion $f(x)$ wird mit $f^{\textcolor{red}{-1}} (x)$ gekennzeichnet. Die hochgestellte $\textcolor{red}{-1}$ ist also das Zeichen für die Umkehrfunktion.
Um eine Umkehrfunktion zu bilden, muss die Funktion zunächst nach $x$ umgestellt werden. Danach werden $x$ und $y$ getauscht, dabei vertauscht sich auch die Definitions- und die Wertemenge.

Schauen wir uns zwei Beispiele an:

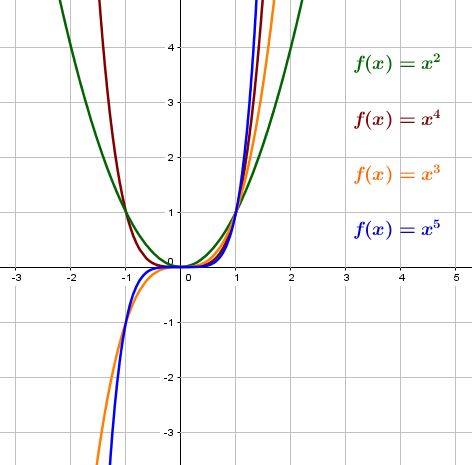
Was ist eine Potenzfunktion? - Wiederholung

Bei einer Potenzfunktion hat die Variable, also der $x$-Wert, einen Exponenten.

Allgemein verlaufen Potenzfunktionen mit positiven Exponenten immer durch den Ursprung. In diesem Text schauen wir uns aber nur die Umkehrfunktionen von solchen Potenzfunktionen an.  

Abbildung: Graphen von Potenzfunktionen mit natürlichen Exponenten

Wie sehen die Umkehrfunktionen von solchen Potenzfunktionen mit positiven Exponenten aus?

Umkehrfunktionen von Potenzfunktionen bilden - Schritt für Schritt

Potenzfunktionen mit ungeradem Exponenten

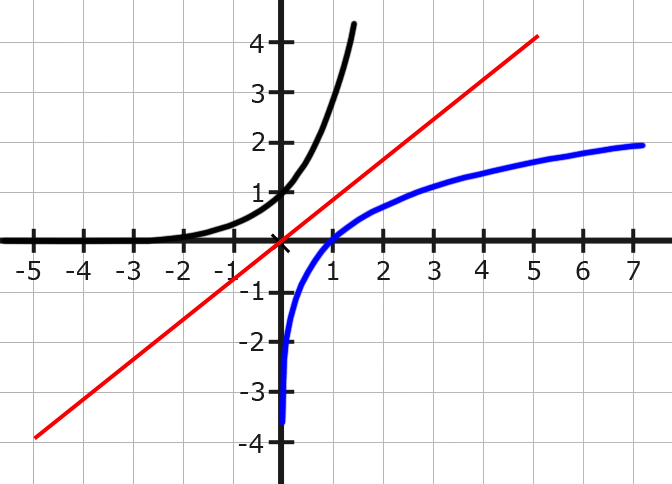
Die Umkehrfunktion der Potenzfunktion $f(x) = x^3$ soll gebildet werden. Wir gehen so vor, wie oben beschrieben:

Beispiel

Hier klicken zum Ausklappen

1. Die Funktion nach $x$ auflösen:

$y = x^3 ~~~~~~~|\sqrt[3]{~~}$
$\sqrt[3]{y}= x$

2. $x$ und $y$ tauschen:

$y= \sqrt[3]{x}$   bzw.   $f^{-1}(x) =y= \sqrt[3]{x}$

Abbildung: Funktion $f(x) = x^3 $ und die Umkehrfunktion $f^{-1}(x)= \sqrt[3]{x}$

Bei allen anderen Potenzfunktionen, die einen ungeraden Exponenten haben, kann man genauso vorgehen.

Potenzfunktionen mit geradem Exponenten

Bei Potenzfunktionen, die einen geraden Exponenten haben, muss man anders verfahren, denn jedem $y$-Wert werden zwei $x$-Werte zugeordnet. So ist beispielsweise bei der Funktion $y=x^2$ für den $y$-Wert $y= 4$ sowohl $x=2$ als auch $x=-2$ richtig. Daher muss der Definitionsbereich eingeschränkt werden.

Schauen wir uns dazu die Umkehrfunktion der Funktion $f(x)=x^2$ an:

Beispiel

Hier klicken zum Ausklappen

Es muss zunächst die Definitionsmenge festgelegt werden. Wir wollen die Umkehrfunktion für alle positiven $x$-Werte bilden, $x\ge 0$.

1. Die Funktion nach $x$ auflösen:

$f(x)= x^2 ~~~~~~~|\sqrt[2]{~~}$
$\sqrt[2]{y}= x$

2. $x$ und $y$ tauschen:

$f^{-1}(x)=  \sqrt[2]{x}$,          für alle $x\ge 0$.

Abbildung: Funktion $f(x) = x^2 $ mit Umkehrfunktion $f^{-1}(x)= \sqrt[2]{x}$

Mit den Übungsaufgaben kannst du nun dein neu erworbenes Wissen zum Bilden von Umkehrfunktionen überprüfen. Viel Erfolg dabei!

Video: Simon Wirth

Text: Chantal Rölle