Mit Quadrat- und Kubikwurzeln rechnen
In diesem Lerntext befassen wir uns mit der Frage, was eigentlich eine Quadrat- oder Kubikwurzel ist.
Das Wurzelziehen - Wiederholung
Das Wurzelziehen ist das Gegenteil des Potenzierens. Anstatt Wurzelziehen sagt man auch radizieren. Das mathematische Symbol für das Wurzelziehen ist das Wurzelzeichen: $\sqrt{\textcolor{white}{...}}$
$Potenzieren~~~~~~~~~~~~~~~~~~~~Radizieren$
$\textcolor{red}{8}^\textcolor{blue}{2} = \textcolor{green}{64}~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\sqrt[\textcolor{blue}{2}]{\textcolor{green}{64}} = \textcolor{red}{8}$
gesprochen: Die zweite Wurzel aus vierundsechzig ist acht.
Merke
Eine Wurzel ist gegeben durch:
$\textcolor{red}{a}^\textcolor{blue}{n} = \textcolor{green}{x} \Leftrightarrow \sqrt[\textcolor{blue}{n}]{\textcolor{green}{x}} = \textcolor{red}{a}$
Dabei bezeichnet man $\textcolor{green}{x}$ als den Radikanden und $\textcolor{blue}{n}$ als den Wurzelexponenten.
Was ist eine Quadratwurzel?
Wurzeln, deren Wurzelexponent $2$ ist, bezeichnet man auch als Quadratwurzeln. In der Regel lässt man den Wurzelexponenten $2$ jedoch weg, weil die Quadratwurzel die am häufigsten vorkommende Wurzel ist. Alle Wurzelexponenten, die größer als $2$ sind, müssen immer dazugeschrieben werden.
Beispiel
$\sqrt[2]{49} = 7 \Leftrightarrow \sqrt{49} = 7$
$\sqrt[2]{9} = 3 \Leftrightarrow \sqrt{9} = 3$
$\sqrt[2]{16} = 4 \Leftrightarrow \sqrt{16} = 4$
Die Quadratwurzel aus einer Zahl ist also diejenige Zahl, die zum Quadrat genommen die Zahl unter der Wurzel ergibt. Eine allgemeine Form der Quadratwurzel würde also so aussehen:
Wenn $x \cdot x = y$, dann gilt: $\sqrt{y} = x$
Da das Ziehen der Quadratwurzel in vielen Fällen krumme Zahlen ergibt, berechnest du sie meistens mit Hilfe des Taschenrechners. In diesen Fällen musst du die Zahlen runden:
- $\sqrt{2} \approx 1,4142$
- $\sqrt{10} \approx 3,1623$
Merke
Die Quadratwurzel ist beschrieben durch:
$\textcolor{red}{x}^\textcolor{blue}{2} = \textcolor{green}{y} \Leftrightarrow \sqrt{\textcolor{green}{y}} = \textcolor{red}{x}$
Die Quadratwurzel lässt sich auch aus Brüchen ziehen, indem die Wurzel einzeln von Zähler und Nenner gezogen wird.
- $\sqrt{\frac{4}{9}} = \frac{\sqrt{4}}{\sqrt{9}} = \frac{2}{3}$
- $\sqrt{\frac{16}{4}} = \frac{\sqrt{16}}{\sqrt{4}} = \frac{4}{2} = 2$
Aufgrund des Zusammenhangs von Quadratwurzel und dem Quadrieren (mit Zwei hoch nehmen), kannst du keine Quadratwurzel aus einer negativen Zahl ziehen.
$x^2 = y \sqrt{y} = x$
$x^2$ kann nie eine negative Zahl ergeben:
$(-2)^2 = 4$
$2^2 = 4$
Hinweis
Es ist mathematisch nicht möglich Quadratwurzeln aus negativen Zahlen zu ziehen!
Was ist eine Kubikwurzel?
Die Kubikwurzel unterscheidet sich von der Quadratwurzel durch den Wurzelexponenten.
$Potenzieren~~~~~~~~~~~~~~~~~~~~Radizieren$
$\textcolor{red}{3}^\textcolor{blue}{3} = \textcolor{green}{27}~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\sqrt[\textcolor{blue}{3}]{\textcolor{green}{27}} = \textcolor{red}{3}$
Anstatt die Zahl hoch zwei zu nehmen, fragt die Kubikwurzel nach Zahlen, die hoch drei genommen wurden. Ein weiterer Unterschied zur Quadratwurzel ist, dass du die $\textcolor{blue}{3}$ immer mit an die Wurzel schreiben musst und nicht einfach weglassen darfst.
Beispiel
$4^3 = 64 \rightarrow \sqrt[3]{64} = 4$
$9^3 = 729 \rightarrow \sqrt[3]{729} = 9$
$1^3 = 1 \rightarrow \sqrt[3]{1} = 1$
Merke
Die Kubikwurzel ist beschrieben durch:
$\textcolor{red}{a}^\textcolor{blue}{3} = \textcolor{green}{x} \Leftrightarrow \sqrt[\textcolor{blue}{3}]{\textcolor{green}{x}} = \textcolor{red}{a}$
Im Gegensatz zur Quadratwurzel lässt sich die Kubikwurzel auch aus negativen Zahlen ziehen:
$(-3)^3 = - 27$
$\sqrt[3]{-27} = -3$
Wie schreibe ich eine Wurzel als Potenz? - Vorgehensweise
Merke
Eine Wurzel drückt eine umgekehrte Potenz aus.
Wurzeln und Potenzen hängen sehr stark zusammen. Zum einen drückt eine Wurzel praktisch eine umgekehrte Potenz aus. Zum anderen lassen sich Wurzeln auch als Potenzen schreiben:
$\sqrt[3]{64} = 64^{\frac{1}{3}}= 4$
$\sqrt[2]{81} = 81^{\frac{1}{2}}= 9$
Merke
Wurzeln lassen sich als Potenzen schreiben, indem man den Radikand als Basis und den Kehrwert des Wurzelexponenten als Exponenten nimmt:
$\sqrt[\textcolor{blue}{n}]{\textcolor{green}{x}} = \textcolor{green}{x}^{\frac{1}{\textcolor{blue}{n}}}$
Dein neu erlerntes Wissen zu Qudratwurzeln und Kubikwurzeln kannst du nun mit unseren Übungsaufgaben testen! Wir wünschen dir dabei viel Erfolg und Spaß!
Weitere interessante Inhalte zum Thema
-
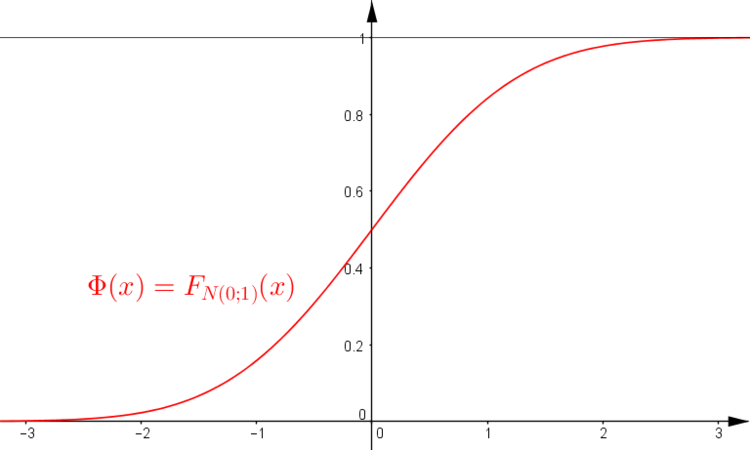
Verteilungsfunktion der Normalverteilung
Vielleicht ist für Sie auch das Thema Verteilungsfunktion der Normalverteilung (Normalverteilung) aus unserem Online-Kurs Stochastik interessant.
-
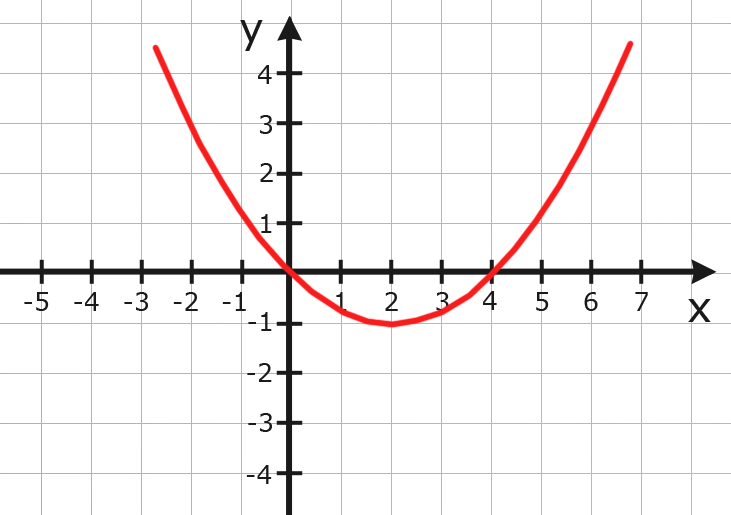
Kurvenschar Wurzel 2
Vielleicht ist für Sie auch das Thema Kurvenschar Wurzel 2 (Funktionsuntersuchung ganzrationaler Kurvenscharen) aus unserem Online-Kurs Grundlagen der Analysis (Analysis 1) interessant.