Verhältnis zwischen 2 Winkeln - Winkeltypen im Überblick

In diesem Text wird dir erklärt, was ein Scheitel-, Neben-, Stufen- und Wechselwinkel ist. Diese beschreiben je ein Verhältnis zwischen zwei Winkeln. Kennt ihr die verschiedenen Winkelarten, könnt ihr verschiedene Winkelgrößen einfach bestimmen.

Was ist ein Scheitelwinkel?

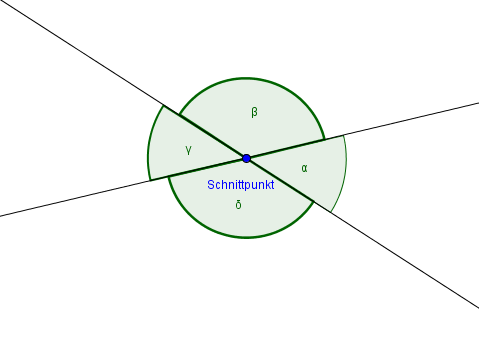
Wenn sich zwei Geraden schneiden, ergeben sich an dem Schnittpunkt vier Winkel. 

Abbildung: zweier Geraden mit einem Schnittpunkt und vier Winkeln

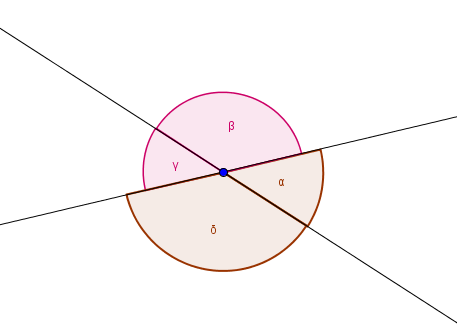
Wie du erkennst, entstehen die vier Winkel $\alpha, \beta, \gamma$ und $\delta$. Wenn wir die Abbildung weiter betrachten, fällt uns auf, dass $\alpha$ und $\gamma$ gleich groß sind, ebenso wie die Winkel $\beta$ und $\delta$.

Wenn sich zwei Graphen schneiden, bezeichnet man die Winkel, die sich gegenüberliegen, als Scheitelwinkel. Die Scheitelwinkel sind gleich groß!

Abbildung: Scheitelwinkel

Was ist ein Nebenwinkel?

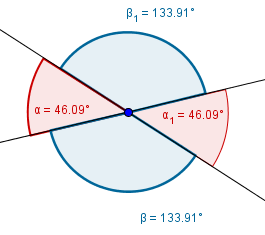
Nebenwinkel sind zwei nebeneinander liegende Winkel, die beim Schneiden zweier Geraden entstehen. Die Summe von zwei Nebenwinkeln beträgt $180^\circ$. Dies kannst du an der Abbildung erkennen.

Abbildung: Nebenwinkel

Wenn wir zwei nebeneinanderliegende Winkel zusammen rechnen, erhalten wir einen $180^\circ$ großen Winkel. Einen solchen Winkel bezeichnet man auch als gestreckten Winkel.
In der Abbildung erkennen wir, dass $\textcolor{brown}{\alpha+ \delta = 180^\circ}$ und auch $\textcolor{red}{\gamma + \beta = 180^\circ}$.

Die anderen beiden Winkel, die nebeneinander liegen, sind auch Nebenwinkel und somit $180^\circ $groß.  Also sind zum Beispiel $\alpha$ und $\beta$ zusammen $180^\circ$ groß .

Was ist ein Stufenwinkel?

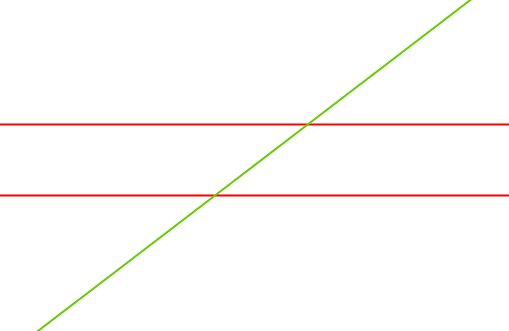
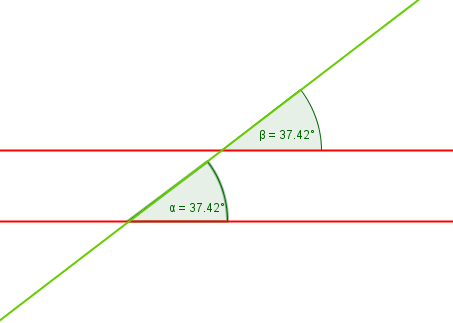
Ein Stufenwinkel entsteht, wenn zwei Parallelen von einer Geraden geschnitten werden. Schauen wir uns als erstes eine Abbildung an.

Abbildung: zwei Parallelen geschnitten von einer Geraden

Die zwei Parallelen, hier in $\textcolor{red}{rot}$ gekennzeichnet, werden von einer anderen Geraden, hier in $\textcolor{green}{grün}$ gekennzeichnet, geschnitten. Damit erhalten wir zwei Schnittpunkte mit je vier Winkeln, also insgesamt acht Winkel. 
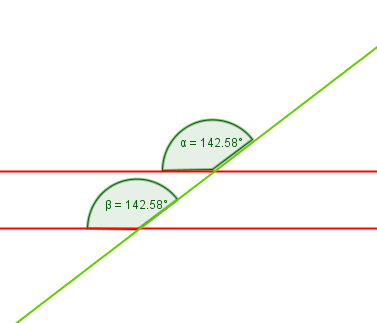
Wir wissen schon, dass die gegenüberliegenden Winkel Scheitelwinkel heißen und damit gleich groß sind. Auch die Stufenwinkel sind gleich groß. Wie das Wort Stufenwinkel schon sagt, liegen diese wie Stufen auf oder unter den Parallelen. In der Abbildung können wir erkennen, dass die Stufenwinkel gleich groß sind.

 Abbildung: Stufenwinkel

Die Stufenwinkel sind gleich groß, da die Gerade die zwei Parallelen mit dem gleichen Winkel schneidet. So sind zum Beispiel auch diese zwei Winkel Stufenwinkel und damit gleich groß:

Abbildung: Stufenwinkel 2

Was ist ein Wechselwinkel?

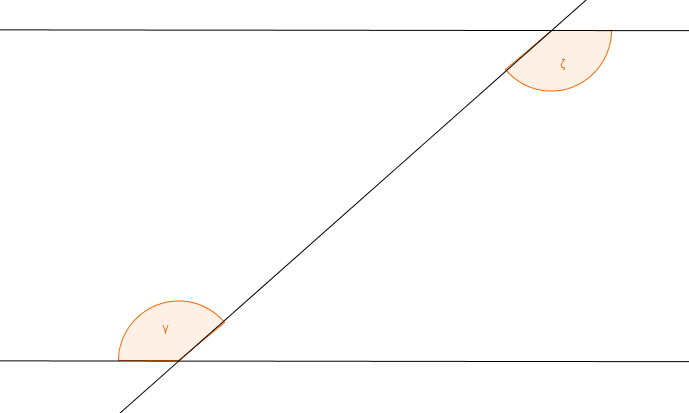
Ein Wechselwinkel entsteht genau wie ein Stufenwinkel, wenn zwei Parallelen von einer Geraden geschnitten werden.

Wir wissen schon, dass die jeweiligen Stufenwinkel gleich groß sind. Können wir noch mehr gleich große Winkel in der Abbildung erkennen?

Abbildung: zwei Parallelen geschnitten von einer Geraden

Bei genauer Betrachtung fällt auf, dass noch weitere Winkel gleich groß sind:

Abbildung: Wechselwinkel

Da die Stufenwinkel und auch die sich gegenüberliegenden Winkel (Scheitelwinkel) gleich groß sind, muss auch der Wechselwinkel zwischen der Geraden und den beiden Parallelen gleich groß sein.

Besondere Winkel - Übersicht

Merke

Hier klicken zum Ausklappen

Scheitelwinkel

Wenn sich zwei Graphen schneiden, bezeichnet man die Winkel, die sich gegenüberliegen, als Scheitelwinkel. Die Scheitelwinkel sind gleich groß!

Abbildung: Scheitelwinkel

Nebenwinkel

Winkel, die an einer Geraden nebeneinander liegen, bezeichnet man als Nebenwinkel. Die Summe der zwei Winkel beträgt $180^\circ$.

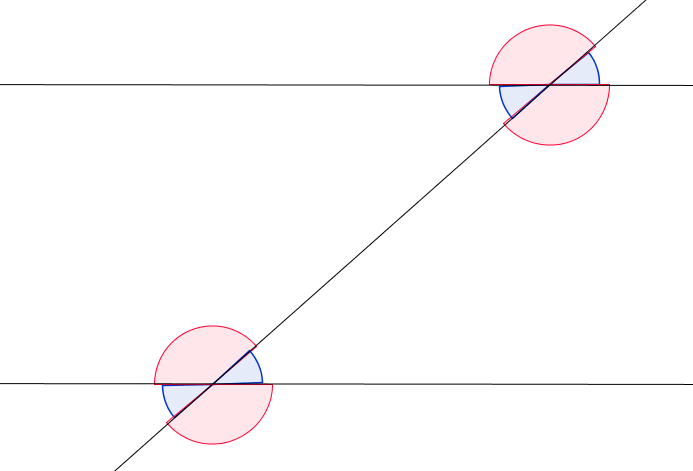
Wechselwinkel und Stufenwinkel

Wenn zwei Parallelen von einer Geraden geschnitten werden, entstehen Wechselwinkel und Stufenwinkel. Insgesamt haben die acht verschiedenen Winkel nur zwei unterschiedliche Winkelgrößen.

Abbildung: Stufenwinkel und Wechselwinkel

Jetzt kennst du die verschiedenen Winkelarten in der Mathematik. Dein neu erlerntes Wissen kannst du mit unseren Übungen festigen. Wir wünschen dir dabei viel Spaß!