Wie berechnet man die Diagonale von Vierecken/Quadraten?
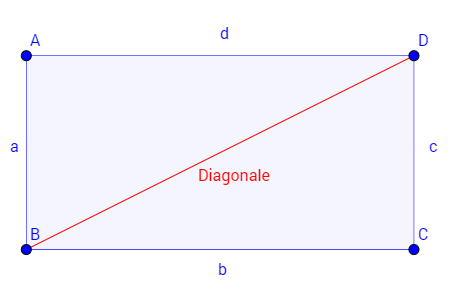
Eine Diagonale von einem Viereck verbindet zwei gegenüberliegende Punkte. In diesem Text erklären wir dir, wie die Länge einer Diagonale berechnet werden kann.
Eine Diagonale ist die Verbindungsstrecke zweier Punkte, die nicht miteinander verbunden sind.
Diagonalen berechnen - Formel
Merke
$d=\sqrt{ a^2+b^2}$
Die Länge der Diagonale eines Rechtecks mit den Seitenlängen $a$ und $b$ wird berechnet, indem die beiden Längen zum Quadrat genommen addiert werden und dann daraus die Wurzel gezogen wird. Wie diese Formel zustande kommt, erklären wir jetzt:
Berechnung von Diagonalen - Herleitung der Formel
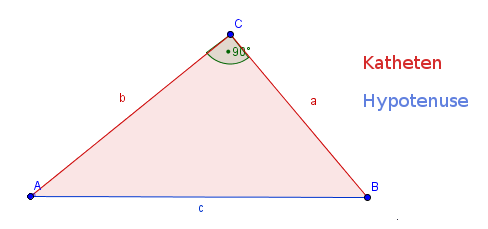
Die Formel kann ganz einfach mit dem Satz des Pythagoras hergeleitet werden:
$c^2 = a^2 +b^2$
Da bei einem Rechteck ein rechter Winkel vorliegt, ist die Diagonale die Hypotenuse und wir können die Formel umschreiben:
$d^2=a^2+b^2$
Nun lösen wir die Formel nach $d$ auf:
$d= \sqrt{a^2+b^2}$
Auf dieser Seite kannst du den Beweis des Satz des Pythagoras nochmal nachlesen.
Wie berechnet man die Diagonalenlänge? - Beispielaufgabe
Beispiel
Das Rechteck $ABCD$ ist gegeben. Dabei sind die Seiten $a=3cm$ und $b=4cm$ bekannt. Berechne die Länge der Diagonale!
Wir setzen die Seitenlängen in die Formel ein:
$d=\sqrt{ a^2+b^2}$
$d= \sqrt{3cm^2 + 4cm^2}$
$d= \sqrt{9cm^2 + 16cm^2}$
$d= \sqrt{25cm^2}$
$d= 5cm$
Wie berechnet man die Seitenlänge mit der Diagonalen? - Beispielaufgabe
Beispiel
Wir haben die Diagonalenlänge eines Quadrates gegeben und sollen die Seitenlänge des Quadrates ermitteln.
$d= 4cm, a=?$
Wir nehmen die Grundformel:
$d=\sqrt{ a^2+b^2}$
Da die beiden Seitenlängen $a$ und $b$ gleich lang sind, nennen wir $b$ auch $a$:
$d=\sqrt{ a^2+a^2} = \sqrt{ 2\cdot a^2}= \sqrt{2}\cdot a$
Nun stellen wir die Formel nach $a$ um, da dies gesucht ist:
$d =\sqrt{2}\cdot a~~~~~~~~~|:\sqrt{2}$
$\frac{d}{\sqrt{2}}= a$
Jetzt können wir die Länge der Diagonale einsetzen:
$a= \frac{4}{\sqrt{2}} \approx 2,83$
Die Seitenlänge des Quadrats beträgt ca. $2,83 cm$ lang.
Mit den Übungsaufgaben kannst du dein Wissen weiter vertiefen. Viel Erfolg dabei!
Video: Simon Wirth
Text: Chantal Rölle
Weitere interessante Inhalte zum Thema
-
Einheitsmatrix
Vielleicht ist für Sie auch das Thema Einheitsmatrix (Matrizen) aus unserem Online-Kurs Analytische Geometrie / Lineare Algebra (Agla) interessant.
-
Abstände von Punkten
Vielleicht ist für Sie auch das Thema Abstände von Punkten (Lagebeziehungen und Abstände) aus unserem Online-Kurs Analytische Geometrie / Lineare Algebra (Agla) interessant.