Kürzen und Erweitern von Brüchen - Regeln einfach erklärt
Zwei der wichtigsten Methoden im Umgang mit Brüchen sind das Kürzen und das Erweitern von Brüchen. Im Folgenden schauen wir uns beide Methoden ausführlich an.
Wie kürzt man Brüche?
Um zu verstehen, wie das Kürzen von Brüchen funktioniert und was uns diese Methode bringt, betrachten wir folgendes Beispiel.
Beispiel
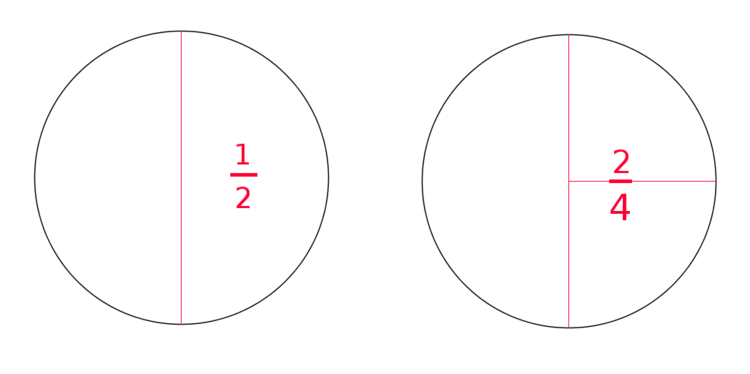
Eine Pizza soll zwischen zwei Leuten aufgeteilt werden. Eine ziemlich simple Aufgabe, da die Pizza einfach halbiert werden muss. Durch das Halbieren erhalten wir zwei Stücke Pizza, die jeweils den Anteil $\frac{1}{2}$ haben. Da man dieses große Pizzastück nur schwer mit der Hand essen kann, teilen wir die Hälften nochmal auf. Insgesamt haben wir die Pizza also in vier Viertel geteilt, von denen jeweils zwei Viertel für eine Person sind. Das heißt, dass eine halbe Pizza und zwei viertel Stücke einer Pizza gleich viel sind.
Brüche können also unterschiedlich aussehen, aber demselben Wert entsprechen:
- $\frac{1}{2} = 0,5$
- $\frac{2}{4} = 0,5$
Demnach können wir die Brüche auch gleichsetzen: $\frac{2}{4} = \frac{1}{2}$
Beim Gleichsetzen dieser Brüche haben wir $\frac{2}{4}$ auf $\frac{1}{2}$ gekürzt. Mathematisch ist dies möglich, da beide Brüche für dieselbe Zahl stehen, nämlich $0,5$.
Beim Kürzen von Brüchen geht es also darum, einen Bruch so umzuwandeln, dass die Zahlen in Zähler und Nenner möglichst klein werden, der mathematische Ausdruck aber noch korrekt ist.
Merke
Beim Kürzen von Brüchen sollen die Zahlen in Zähler und Nenner möglichst klein werden.
Doch wie funktioniert das Kürzen? Muss man sich etwa jedes Mal eine Pizza vorstellen und in einzelne Stücke teilen? Die Antwort ist zum Glück nein, denn das Kürzen von Brüchen funktioniert auch rein rechnerisch.
Um von $\frac{2}{4}$ auf $\frac{1}{2}$ zu kommen werden Zähler und Nenner durch $2$ geteilt.
$\large{\frac{2}{4} = \frac{2\textcolor{red}{:2}}{4\textcolor{red}{:2}} = \frac{1}{2} = 0,5}$
Merke
Der Wert des Bruchs ändert sich nicht, wenn sowohl Zähler als auch Nenner durch dieselbe Zahl geteilt werden.
Beim Kürzen von Brüchen teilst du Zähler und Nenner durch den größten gemeinsamen Teiler. Diesen Teiler nennt man auch Kürzungszahl.
Die Kürzungszahl oder auch der Teiler ist nichts anderes als die Zahl, durch die sich die Zahl im Zähler und die Zahl im Nenner teilen lassen, ohne eine Kommazahl zu ergeben. Ein Bruch sollte immer vollständig gekürzt werden, das heißt: Nach dem Kürzen gibt es keine weiteren Möglichkeiten, Zähler und Nenner durch einen gemeinsamen Teiler zu teilen.
Beispiel
$\large{\frac{4}{8} = \frac{4:4}{8:4} = \frac{1}{2}}$
$\large{\frac{27}{18} = \frac{27:9}{18:9} = \frac{3}{2}}$
$\large{\frac{14}{6} = \frac{14:2}{6:2} = \frac{7}{3}}$
$\large{\frac{256}{8} = \frac{256:8}{8:8} = \frac{32}{1}}$
Wie erweitert man Brüche?
Das Erweitern von Brüchen ist das mathematische Gegenstück zum Kürzen. Während es beim Kürzen von Brüchen darum geht, die Zahlen in Zähler und Nenner möglichst klein zu bekommen, vergrößern wir beim Erweitern von Brüchen die Werte von Zähler und Nenner.
Merke
Das Erweitern von Brüchen ist das mathematische Gegenstück zum Kürzen von Brüchen.
Beim Erweitern von Brüchen müssen wir die Zahlen in Zähler und Nenner mit einem bestimmten Wert multiplizieren:
$\large{\frac{1}{2} = \frac{1 \textcolor{red}{\cdot 2}}{2 \textcolor{red}{\cdot 2}} = \frac{2}{4} = 0,5}$
Im Gegensatz zum Kürzen, dass in der Regel vollständig passiert, haben wir beim Erweitern von Brüchen keine Grenzen. Wir könnten den obigen Bruch also auch so erweitern:
$\large{\frac{1}{2} = \frac{1 \textcolor{red}{\cdot 30}}{2 \textcolor{red}{\cdot 30}} = \frac{30}{60} = 0,5}$
Merke
Brüche werden erweitert, indem Zähler und Nenner mit derselben Zahl multipliziert werden.
Beispiel
$\large{\frac{3}{4} = \frac{3 \cdot 3}{4 \cdot 3} = \frac{9}{12}}$
$\large{\frac{1}{9} = \frac{1 \cdot 5}{9 \cdot 5} = \frac{5}{45}}$
$\large{\frac{2}{3} = \frac{2 \cdot 2}{3 \cdot 2} = \frac{4}{6}}$
Du hast bis hier hin schon sehr viel über das Kürzen und Erweitern von Brüchen gelernt. Zur Vertiefung dieses Themas schau auch noch einmal in die Übungen! Viel Erfolg dabei!
Weitere interessante Inhalte zum Thema
-
Chemisches Gleichgewicht und Kinetik
Vielleicht ist für Sie auch das Thema Chemisches Gleichgewicht und Kinetik (Chemische Reaktionen) aus unserem Online-Kurs Anorganische Chemie interessant.
-
Vervielfachen von Matrizen
Vielleicht ist für Sie auch das Thema Vervielfachen von Matrizen (Rechenregeln für Matrizen) aus unserem Online-Kurs Analytische Geometrie / Lineare Algebra (Agla) interessant.