Flächeninhalt und Umfang eines Drachenvierecks berechnen

In diesem Text erfährst du alles, was du über Drachenvierecke wissen solltest: Welche Eigenschaften sie haben und wie du den Flächeninhalt und den Umfang berechnen kannst.

Drachenviereck - Eigenschaften und Besonderheiten 

Ein Drachenviereck hat immer eine Spiegelachse in der Mitte. Die Spiegelachse wird durch die Diagonale gebildet. Das typische Drachenviereck sieht so aus:

Abbildung: Drachenviereck mit zwei Diagonalen

Dieses Drachenviereck ist symmetrisch zu einer Diagonalen. Die Diagonale ist hier blau gekennzeichnet. Die andere Diagonale ist grün gekennzeichnet. Trennen wir das Viereck durch die grüne Diagonale, entstehen zwei gleichschenklige Dreiecke.

Woher der Name Drachenviereck kommt,  kannst du dir vielleicht schon denken:

Abbildung: Drache

Da Drachenvierecke eine Spiegelachse haben, ergeben sich weitere Besonderheiten.

1.  die Seiten, die sich gegenüberliegen, sind gleich lang
2.  die beiden Diagonalen stehen senkrecht aufeinander
3.  die Spiegelachse halbiert die andere Diagonale

Berechnungen am Drachenviereck - Formeln

Schauen wir uns ein paar Formeln zu Berechnungen an einem Drachenviereck an:

Die Bedeutung der Abkürzungen $h, c, a $ und $b$ ist hier dargestellt:

Abbildung: Drache mit Bezeichnungen

Berechnungen am Drachenviereck - Formeln herleiten

Hier schauen wir uns an, wie die Formeln zur Berechnung erklärt werden können.

Flächeninhalt berechnen

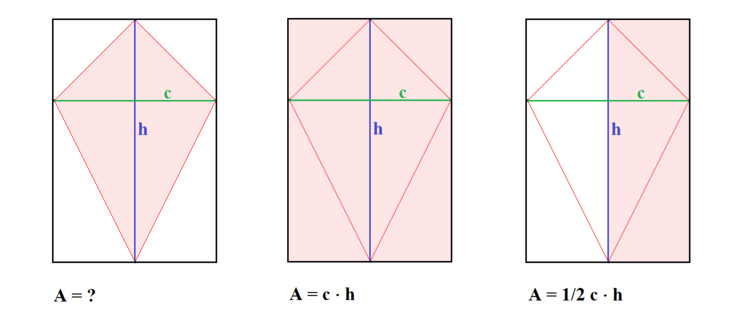
Betrachten wir folgendes Bild:

Abbildung: Flächeninhalt Drache

Der Flächeninhalt von einem Drachenvieleck ist die Höhe (also die Länge der einen Diagonale) mal der Breite (die Länge der anderen Diagonale) geteilt durch zwei. In der Abbildung können wir erkennen, dass der Flächeninhalt von dem Drachenviereck in die Hälfte des Rechtecks hineinpasst. So kannst du dir die Formel ganz einfach merken.

Umfang berechnen

Es ist klar, dass alle Seitenlängen einfach addiert werden müssen. Da die Längen zweimal vorkommen, ergibt sich:

$U = 2\cdot (a+b)$

Beispielaufgabe - Berechnungen am Drachenviereck

Schauen wir uns eine Beispielaufgabe an:

Beispiel

Hier klicken zum Ausklappen

Berechne den Flächeninhalt und den Umfang dieses Drachenvierecks:

Abbildung: Drache mit Längenangaben

Den Umfang berechnen wir, indem wir die Längen der Seiten zusammenrechnen:

$U = 2 \cdot (20 cm + 34 cm) = 108 cm$

Den Flächeninhalt erhalten wir, indem wir die Höhe mal die Breite rechnen und durch zwei teilen.

$A = \frac{1}{2} *42 cm \cdot 32 cm = 672 cm^2$

Mit den Übungsaufgaben kannst du dich testen. Viel Erfolg dabei!