Wie stellt man Formeln um? - Regeln einfach erklärt
In diesem Text erklären wir dir, wie man Gleichungen bzw. Formeln umstellen oder umformen kann.. Dabei gehen wir auf viele Beispiele und Regeln zum Formeln Umstellen ein und geben dir Übungsaufgaben mit Lösungen.
Wie stellt man Gleichungen und Formeln um? - Regeln
Formeln dienen der Berechnung von bestimmten Größen, zum Beispiel des Flächeninhalts:
Beispiel
$A= h \cdot b \rightarrow$ Der Flächeninhalt ist gleich Höhe mal Breite.
Das Umstellen von Formeln ist ein wichtiges Werkzeug in der Mathematik. Es dient dazu, Sachzusammenhänge ineinander umzuformen.
Formeln, die meist nur aus Variablen bestehen, können umgeformt werden. So kann die Formel des Flächeninhalts beispielsweise nach der Höhe umgestellt werden.
Beispiel
$A= h \cdot b~~~~~~~~~~~~~~~~~~~~~~~~~~~~|\textcolor{blue}{:b}$
$\Leftrightarrow A \textcolor{blue}{:b} = h \cdot b \textcolor{blue}{:b}$
$\Leftrightarrow A : b = h$
Wir haben die Formel nach der Höhe umgestellt. $\rightarrow$ Die Höhe ist gleich dem Flächeninhalt geteilt durch die Breite.
Das Gleichheitszeichen besagt, dass beide Seiten gleich sind. Auch wenn die Seiten anders aussehen, steht links und rechts vom Gleichheitszeichen im Endeffekt das Gleiche. Damit die Gleichheit nicht verletzt wird, müssen wir bei der Umformung auf beiden Seiten jeweils das Gleiche machen. Diese Vorgehensweise nennt man Äquivalenzumformung.
Hinweis
Bei der Umformung von Formeln arbeiten wir mit der Äquivalenzumformung. Dies bedeutet, dass auf beiden Seiten des Gleichheitszeichens das Gleiche (Äquivalente) hinzukommt, weggenommen, geteilt oder mal genommen wird.
Formelumstellung - Beispielaufgabe zur Masse
In der Physik gibt es viele Formel, die den Zusammenhang zwischen verschiedenen Größen beschreiben. Somit gibt es auch eine Formel für die Kraft: $F =m \cdot a$, die Kraft ist gleich der Masse mal der Beschleunigung.
Wir haben die Kraft ($F= 10 N$) und die Beschleunigung ($a= 9,81\frac{m}{s^2}$) eines Körpers gegeben und sollen die Masse des Körpers berechnen.
Zuerst formen wir die Formel nach der Masse hin um.
$F = m\cdot a~~~~~~~~~|:a$
$\frac {F}{a}= m$
Nun können wir die Angaben für Kraft und Beschleunigung einsetzen und erhalten die Masse:
$\frac {F}{a}= m$
$m = \frac {10 N}{9,81\frac{m}{s^2}}= \frac {10 \frac{kg\cdot m}{s^2}}{9,81\frac{m}{s^2}} \approx 1,02 kg$
Hinweis
In der Schule geht ihr oft anders vor. Meist werden zuerst die Angaben aus der Aufgabenstellung in die Formel eingesetzt und dann wird mit den Zahlen umgeformt. Dabei können jedoch Rechenfehler passieren. Also probiere es doch aus, die Formeln immer zuerst nach dem Gesuchten umzuformen und danach die Angaben einzusetzen.
Formelumstellung - Beispielaufgabe zur Geschwindigkeit
Nina ist mit ihrer Familie ans Meer gefahren. Die Gesamtstrecke betrug $350km$ und sie sind mit einer Durchschnittsgeschwindigkeit von $90 \frac{km}{h}$ gefahren. Wie lange hat die Familie gebraucht, um ans Meer zu kommen?
Um die Aufgabe lösen zu können, benötigen wir die Formel für die Geschwindigkeit:
$v= \frac{s}{t}$
Die Geschwindigkeit ist die Strecke durch die Zeit.
Versuche die Formel nach der Zeit ($t$) umzuformen und setze dann die Zahlen ein. Danach kannst du dein Ergebnis mit der Lösung vergleichen.
Vertiefung
Lösung
$v= \frac{s}{t}~~~~~~~~~~~~~|\cdot t$
$\Leftrightarrow v\cdot t = s~~~~~|:v$
$\Leftrightarrow t = \frac {s}{v}$
$t = \frac {s}{v}= \frac{350km}{90\frac{km}{h}}\approx 3,89h$
$0,89h$ in Minute umrechnen:
$0,89h \cdot 60 \frac{h}{min}= 53,4 min$
Die Familie war ca. 3 Stunden und 55 Minuten unterwegs.
Das Umstellen von Formeln und Gleichungen ist in Mathe ein bedeutsames Werkzeug. Mit den Übungsaufgaben kannst du weitere Umformungen und die Regeln zum Umstellen von Formeln online einüben. Viel Erfolg dabei!
Weitere interessante Inhalte zum Thema
-
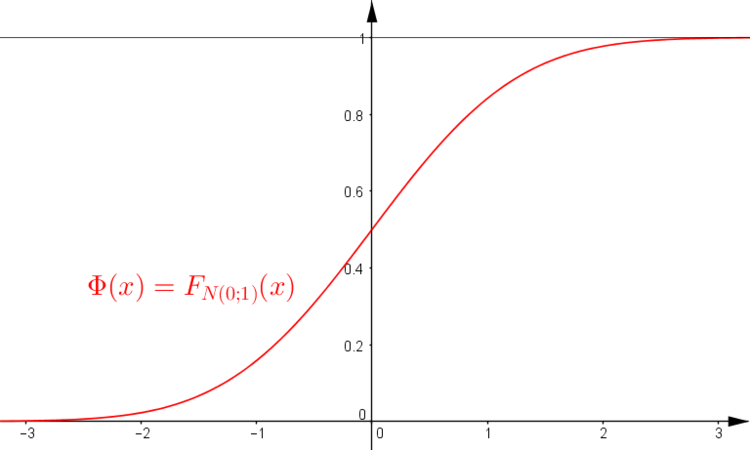
Verteilungsfunktion der Normalverteilung
Vielleicht ist für Sie auch das Thema Verteilungsfunktion der Normalverteilung (Normalverteilung) aus unserem Online-Kurs Stochastik interessant.
-
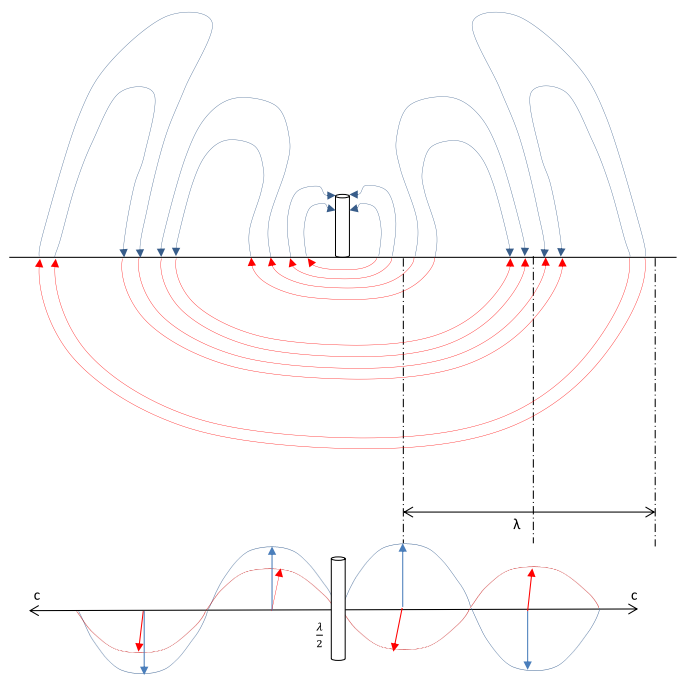
Wellenausbreitung eines strahlenden Dipols
Vielleicht ist für Sie auch das Thema Wellenausbreitung eines strahlenden Dipols (Elektromagnetische Wellen) aus unserem Online-Kurs Elektromagnetismus interessant.