Höhe, Volumen und Fläche beim Kegelstumpf berechnen

In diesem Lerntext erfährst du alles über den geometrischen Körper des Kegelstumpfs.

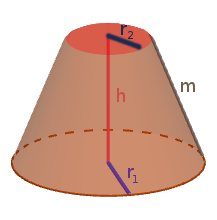
Wie sieht ein Kegelstumpf aus?

Der Kegelstumpf leitet sich vom geometrischen Körper des Kegels ab. Ein Kegel besteht aus einer kreisförmigen Grundfläche und einer Mantelfläche, die der Form eines Kreisauschnitts entspricht.

Ein Kegelstumpf hingegen ist ein Kegel, dessen Spitze weggeschnitten wurde. Daraus ergeben sich einige Unterschiede zur ursprünglichen Kegelform. So besitzt der Kugelstumpf neben der für Kegel typischen kreisförmigen Grundfläche auch eine kreisförmige Deckfläche und eine kürzere Kantenlänge. Die Deckfläche wird auch Schnittfläche genannt. Auch die Mantelfläche hat eine andere Form.

Welche Größen werden am Kegelstumpf berechnet?

Um Berechnungen am Kegelstumpf durchzuführen, stehen uns mehr Größen zur Verfügung als beim normalen Kegel. So unterscheiden wir beim Kegelstumpf den Radius der Grundfläche ($r_1$) und den Radius der Schnittfläche ($r_2$).

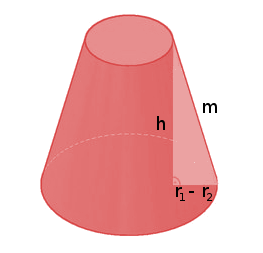
Die Höhe ($h$) des Kegelstumpfs geht vom Mittelpunkt der Grundfläche bis zum Mittelpunkt der Schnittfläche. Die Mantelfläche hat eine viereckige gebogene Form. Die Höhe der Mantelfläche ($m$) entspricht der Seitenlänge des Kegelstumpfs.

Größen im Kegelstumpf

Kegelstumpf - Berechnen der Grund- und Schnittfläche

Grund- und Schnittfläche sind kreisförmig. Um ihren Flächeninhalt zu berechnen, benötigen wir die jeweiligen Radien $r_1$ und $r_2$.

Kegelstumpf - Berechnen der Mantelfläche

Die Mantelfläche eines Kegelstumpfs besitzt eine besondere Form. Man könnte sie als gebogenes Viereck beschreiben. Zur Berechnung der Fläche benötigen wir die Radien der Grund- und der Schnittfläche sowie die Höhe der Mantelfläche.

Kegelstumpf - Berechnen der Höhe

Die Höhe eines Kegelstumpfs lässt sich mithilfe des Satz des Pythagoras berechnen. Zusammen mit der Höhe der Mantelfläche ($m$) und der Differenz der Radien von Grund- und Schnittfläche bildet die Höhe ein rechtwinkliges Dreieck, bei dem gilt:

$(r_1 - r_2)^2 + h^2 = m^2$

Höhe eines Kegelstumpfs berechnen

Stellen wir die Gleichung nach der Höhe um, erhalten wir die Formel zur Berechnung der Höhe eines Kegelstumpfs aus den Radien und der Höhe der Mantelfläche.

Kegelstumpf - Berechnen des Volumens

Die Herleitung des Volumens des Kegelstumpfs ist sehr kompliziert. Es ist vor allem wichtig, dass du lernst die Fomel zur Berechnung des Volumens richtig anzuwenden. Um das Volumen zu berechnen, benötigst du neben den Radien der Grund- und Schnittfläche auch die Höhe des Kegelstumpfs.

Wie du siehst, musst du viele Werte in die Gleichung einsetzen. Pass vor allem darauf auf, dass du wirklich die Radien und nicht die Durchmesser der Grund- und Schnittfläche einsetzt!

Teste dein neu erlerntes Wissen zum Kegelstumpf mit unseren Übungsaufgaben! Wir wünschen dir dabei viel Spaß und Erfolg!