Wie berechnet man Oberfläche und Volumen eines Kegels?

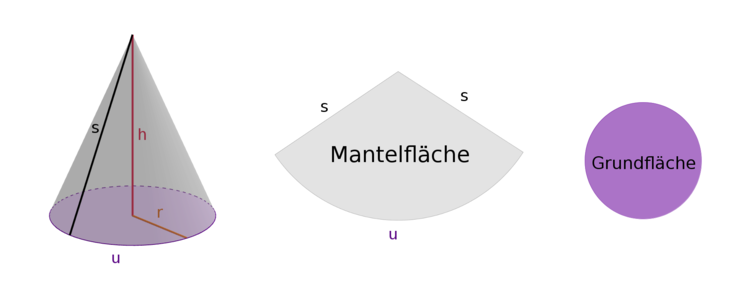
Der Kreiskegel ist ein geometrischer Körper, der wie eine Mischung aus einem Zylinder und einer Pyramide aussieht. Er besitzt eine kreisrunde Grundfläche wie der Zylinder und eine Spitze wie die Pyramide. Die Spitze des Kegels befindet sich genau über dem Mittelpunkt der Grundfläche. Die Mantelfläche ist ein Kreisausschnitt. Wichtige Maße des Kegels sind der Radius $r$ und der Umfang $U$ der Grundfläche, die Höhe $h$ und die Seitenlänge $s$.

Aufbau eines Kreiskegels.

Kreiskegel - Grundfläche berechnen

Die Grundfläche eines Kegels berechnen wir wie die Fläche eines normalen Kreises. Für diese Rechnung benötigen wir also lediglich den Radius.

Kreiskegel - Mantelfläche berechnen

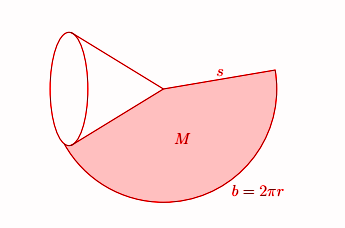
Die Mantelfläche entspricht dem Ausschnitt $b$ eines Kreises mit dem Radius $s$. Die Oberfläche dieses gedachten Kreises ist beschrieben durch:

$A_{großer~Kreis} = \pi \cdot s^2$

Mantelfläche eines Kreiskegels.

Der Umfang des Kreisausschnittes $b$ entspricht dem Umfang der Grundfläche.

$U_{b} = 2 \cdot \pi \cdot r$

Der Umfang des gedachten Kreises, dessen Kreisausschnitt die Mantelfläche ist, ist beschrieben durch:

$U_{großer~Kreis} =2 \cdot \pi \cdot s$

Setzen wir den Umfang, den der Kreisausschnitt, abdeckt in ein Verhältnis mit dem des großen Kreises erhalten wir folgendes:

 $\frac{Umfang~des~Kreisausschnittes}{Umfang~des~gesamten~Kreises} = \frac{2 \cdot \pi \cdot r}{2 \cdot \pi \cdot s} = \frac{r}{s}$

Der Bruch $\frac{r}{s}$ gibt den Anteil des Kreisausschnittes an. Setzen wir diesen Term vor die Formel zur Flächenberechnung des großen Kreises, erhalten wir die Fläche des Kreisausschnittes, also die Mantelfläche:

$A_{großer~Kreis} = \pi \cdot s^2$

$A_{Mantelfläche} = \frac{r}{s} \pi \cdot s^2 = \pi \cdot r\cdot s$

Für den Fall, dass die Seitenlänge $s$ nicht in der Aufgabe gegeben ist, kannst du sie mit Hilfe des Satz des Pythagoras berechnen. Der Radius, die Höhe und die Seitenlänge bilden zusammen ein rechtwinkliges Dreieck, dessen Hypotenuse die Seitenlänge $s$ ist.

$r^2 + h^2 = s^2$

$s= \sqrt[]{r^2 + h^2}$

Kreiskegel - Oberfläche berechnen

Die Oberfläche des Kreiskegels ist die Summe aus Grund- und Mantelfläche.

Kegel - Volumen berechnen

Das Volumen eines Kegels berechnet sich analog zum Volumen einer Pyramide. Neben dem Radius benötigst du beim Errechnen des Volumens die Höhe.

Teste dein neu erlerntes Wissen zur Berechnung von Volumen, Mantelfläche von Kegeln nun mit unseren Übungsaufgaben. Wir wünschen dir viel Erfolg dabei!