Mathematik - Formelsammlung der 9. Klasse
In diesem Text erhältst du einen Überblick über alle Formeln, die du im Mathematikunterricht der 9. Klasse benötigst. Möchtest du zu einer dieser Formeln mehr erfahren, klicke auf die entsprechende Überschrift und du gelangst zur ausführlichen Lernseite zu diesem Thema.
Potenzgesetze
Potenzen mit gleicher Basis
Merke
$\textcolor{black}{ a^m \cdot a^n = a^{m+n}}$
Beispiel: $ \textcolor{black}{2^3 \cdot 2^7 = 2^{10}}$
$\textcolor{black}{\frac{a^m}{a^n} = a^{m-n}}$
Beispiel: $\textcolor{black}{\frac{5^6}{5^2} = 5^{4}}$
$\textcolor{black}{a^{m^n} = a^{m\cdot n}}$
Beispiel: $\textcolor{black}{7^{3^4} = 7^{12}}$
Potenzen mit gleichem Exponenten
Merke
$\textcolor{black}{a^m\cdot b^m = (a\cdot b)^m}$
Beispiel: $\textcolor{black}{5^3\cdot 6^3 = 30^3}$
$\textcolor{black}{\frac{a^m}{b^m} = (\frac{a}{b})^m} $
Beispiel: $\textcolor{black}{\frac{9^8}{3^8} = 3^8 }$
Eine genauere Beschreibung der Potenzgesetze erhältst du auf unserer Übersichtsseite zum Rechnen mit Potenzen.
Quadratische Gleichungen lösen
Merke
p-q-Formel
Für eine Gleichung der Form $x^2 + \textcolor{red}{p} \cdot x + \textcolor{orange}{q} = 0$ gilt.
$x_{1/2} = -\frac{\textcolor{red}{p}}{2}\pm \sqrt{(\frac{\textcolor{red}{p}}{2})^2-\textcolor{orange}{q}}$
Merke
Mitternachstformel
Für eine Gleichung der Form $\textcolor{blue}{a} \cdot x^2 + \textcolor{green}{b} \cdot x + \textcolor{brown}{c} = 0$ gilt:
$x_{1,2} = \frac{\textcolor{green}{-b}~\pm~\sqrt{\textcolor{green}{b}^2~-~4~ \cdot~\textcolor{blue}{a} \cdot~\textcolor{brown}{c}}}{2~ \cdot~\textcolor{blue}{a}}$
Binomische Formeln
Merke
1. binomische Formel
$(\textcolor{blue}{a} \textcolor{green}{+} \textcolor{red}{b})^2 = \textcolor{blue}{a}^2 \textcolor{green}{+} 2 \cdot \textcolor{blue}{a} \cdot \textcolor{red}{b} +\textcolor{red}{b}^2$
2. binomische Formel
$(\textcolor{blue}{a} \textcolor{green}{-} \textcolor{red}{b})^2 = \textcolor{blue}{a}^2 \textcolor{green}{-} 2 \cdot \textcolor{blue}{a} \cdot \textcolor{red}{b} +\textcolor{red}{b}^2$
3. binomische Formel
$(\textcolor{blue}{a} + \textcolor{red}{b}) \cdot (\textcolor{blue}{a} - \textcolor{red}{b}) = (\textcolor{blue}{a}^2 - \textcolor{red}{b}^2)$
Satzgruppe des Pythagoras
Satz des Pythagoras
Merke
$\textcolor{red}{a^2} + \textcolor{red}{b^2} = \textcolor{blue}{c^2}$
Höhensatz des Euklid
Merke
$h^2 = q \cdot p$
Kathetensatz des Euklid
Merke
$b^2 = q \cdot c$
$a^2 = p \cdot c$
Geometrische Körper
Quader
Merke
$O= 2\cdot (a \cdot b + a\cdot c + b\cdot c)$
$V = a \cdot b \cdot c$
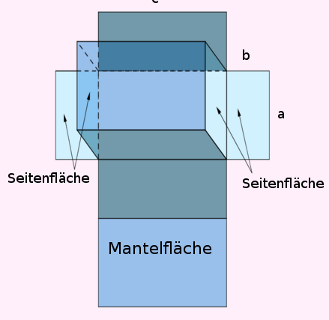
Zylinder
Merke
$A_{Grundfläche} = A_{Deckfläche} = \pi \cdot r^2$
$U_{Grundfläche} = U_{Deckfläche} = 2 \cdot \pi \cdot r$
$A_{Mantelfläche} = U \cdot h = 2 \cdot \pi \cdot r \cdot h$
$O_{Zylinder} = (2\cdot \pi \cdot r^2) + (2 \cdot \pi \cdot r \cdot h)$
$V_{Zylinder} = Grundfläche \cdot Höhe = \pi \cdot r^2 \cdot h$
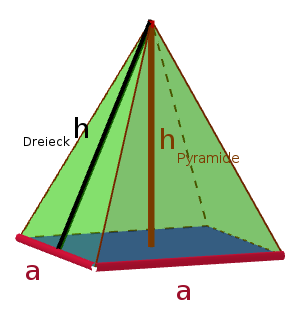
Quadratische Pyramide
Merke
$A_{Grundfläche} = a^2$
$A_{Mantel} = 4 \cdot (\frac{1}{2} \cdot a \cdot h_{Dreieck})$
$O_{Pyramide} =~Grundfläche~+~Mantelfläche~= a^2 + 4 \cdot (\frac{1}{2} \cdot a \cdot h_{Dreieck})$
$V_{Pyramide} = \frac{1}{3} \cdot a^2 \cdot h_{Pyramide}$
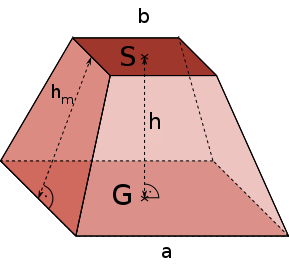
Pyramidenstumpf
Merke
$A_{Grundfläche} = a^2$
$A_{Schnittfläche} = b^2$
$A_{Mantelfläche} = 2 \cdot (a + b) \cdot h_{m}$
$O_{Pyramidenstumpf} = a^2 + b^2 + 2 \cdot (a + b) \cdot h_{m}$
$V_{Pyramidenstumpf} = \frac{h}{3} \cdot a^2 + a\cdot b + b^2$
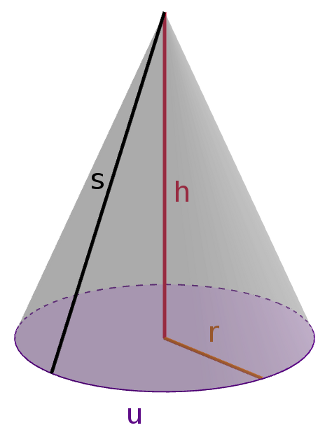
Kreiskegel
Merke
$U_{Grundfläche} = 2 \cdot \pi \cdot r$
$A_{Grundfläche} = \pi \cdot r^2$
$A_{Mantelfläche} = \pi \cdot r\cdot s$
$O_{Kegel} = G + M = (\pi \cdot r^2) + (\pi \cdot r\cdot s)$
$V_{Kegel} = \frac{1}{3} \cdot (\pi \cdot r^2) \cdot h$
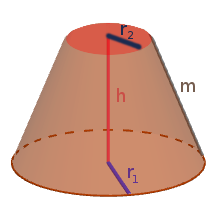
Kegelstumpf
Merke
$A_{Grundfläche} = \pi \cdot (r_1)^2$
$A_{Schnittfläche} = \pi \cdot (r_2)^2$
$A_{Mantelfläche} = (r_1 + r_2) \cdot \pi \cdot m$
$O_{Kegelstumpf} = (\pi \cdot (r_1)^2) + (\pi \cdot (r_2)^2) + ((r_1 + r_2) \cdot \pi \cdot m)$
$V_{Kegelstumpf} = \frac{h \cdot \pi}{3} \cdot (~(r_1)^2 + r_1 \cdot r_2 + (r_2)^2)$
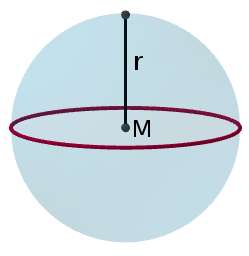
Kugel
Merke
$U_{Kugel}= 2\cdot \pi \cdot r = \pi \cdot d$
$O_{Kugel}= 4\cdot \pi \cdot r^2 $
$V_{Kugel}= \frac{4}{3} \cdot \pi \cdot r^3$
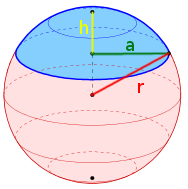
Kugelsegment
Merke
$O_{Kugelsegment} = \pi \cdot (2 \cdot r \cdot h + a^2)$
$V_{Kugelsegment} = \frac{h^2 \cdot \pi}{3} \cdot (3\cdot r - h)$
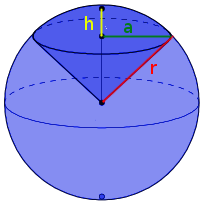
Kugelausschnitt
Merke
$O_{Kugelausschnitt} = \pi \cdot r \cdot (a + 2\cdot h)$
$V_{Kugelausschnitt} = \frac{2\cdot \pi \cdot r^2 \cdot h}{3}$
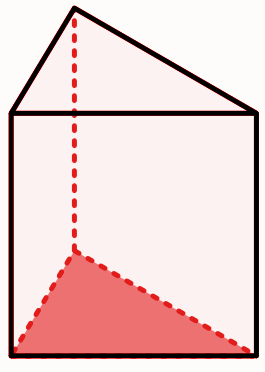
Prisma
Merke
$A_{Mantel} = U_{Grundfläche} \cdot h$
$O_{Prisma} = 2\cdot A_{Grundfläche} + A_{Mantelfläche}$
$V_{Prisma} = G ~ \cdot ~h$
Platonische Körper
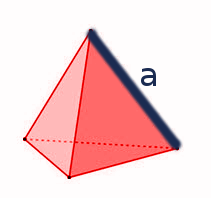
Tetraeder
Merke
$V_{Tetraeder} \approx 0,1179 \cdot a^3$
$O_{Tetraeder} \approx 1,7321 \cdot a^2$
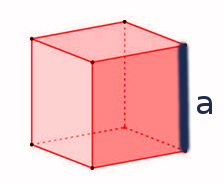
Hexaeder
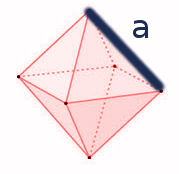
Oktaeder
Merke
$V_{Oktaeder} \approx 0,4714 \cdot a^3$
$O_{Oktaeder} \approx 3,4641 \cdot a^2$
Dodekaeder
Merke
$V_{Dodekaeder} \approx 7,6631 \cdot a^3$
$O_{Dodekaeder} \approx 20,6457 \cdot a^2$
Ikosaeder
Weitere interessante Inhalte zum Thema
-
Klassen
Vielleicht ist für Sie auch das Thema Klassen (Beschreibende Statistik) aus unserem Online-Kurs Stochastik interessant.
-
Quadratische Funktionen mit pq-Formel und Mitternachtsformel lösen
Vielleicht ist für Sie auch das Thema Quadratische Funktionen mit pq-Formel und Mitternachtsformel lösen (Gleichungen lösen) aus unserem Online-Kurs Vorkenntnisse zur Analysis interessant.